maths and algorithms behind photo-realistic graphics
dr. jon denning
assistant professor of cse
taylor university
Frank S. Brenneman Lecture Series
|
warning: there will be equations do not be afraid of them |
|
goal of photo-realism: produce a computer-generated image that is indistinguishable from an actual photograph |
 [ bertil pinewood chair, 2006, ikea link ]
|
 [ mikhalenko link ]
|
 [ viktor fretyán link ]
|
 [ valkyrie link ]
|
 [ valkyrie link ]
|
 [ valkyrie link ]
|
 [ frank tzeng link ]
|
 [ luc bégin link ]
|
 [ jungwon park link ]
|
|
[ chris jones link ]
|
|
[ andrew price link ]
|
 [ youyudetun, link ]
|
the good
|
today we use the same principles behind the earliest cg  [ martin newell, link ]
|
|
rendering system : light simulation emit from source, enter camera, bounce around scene 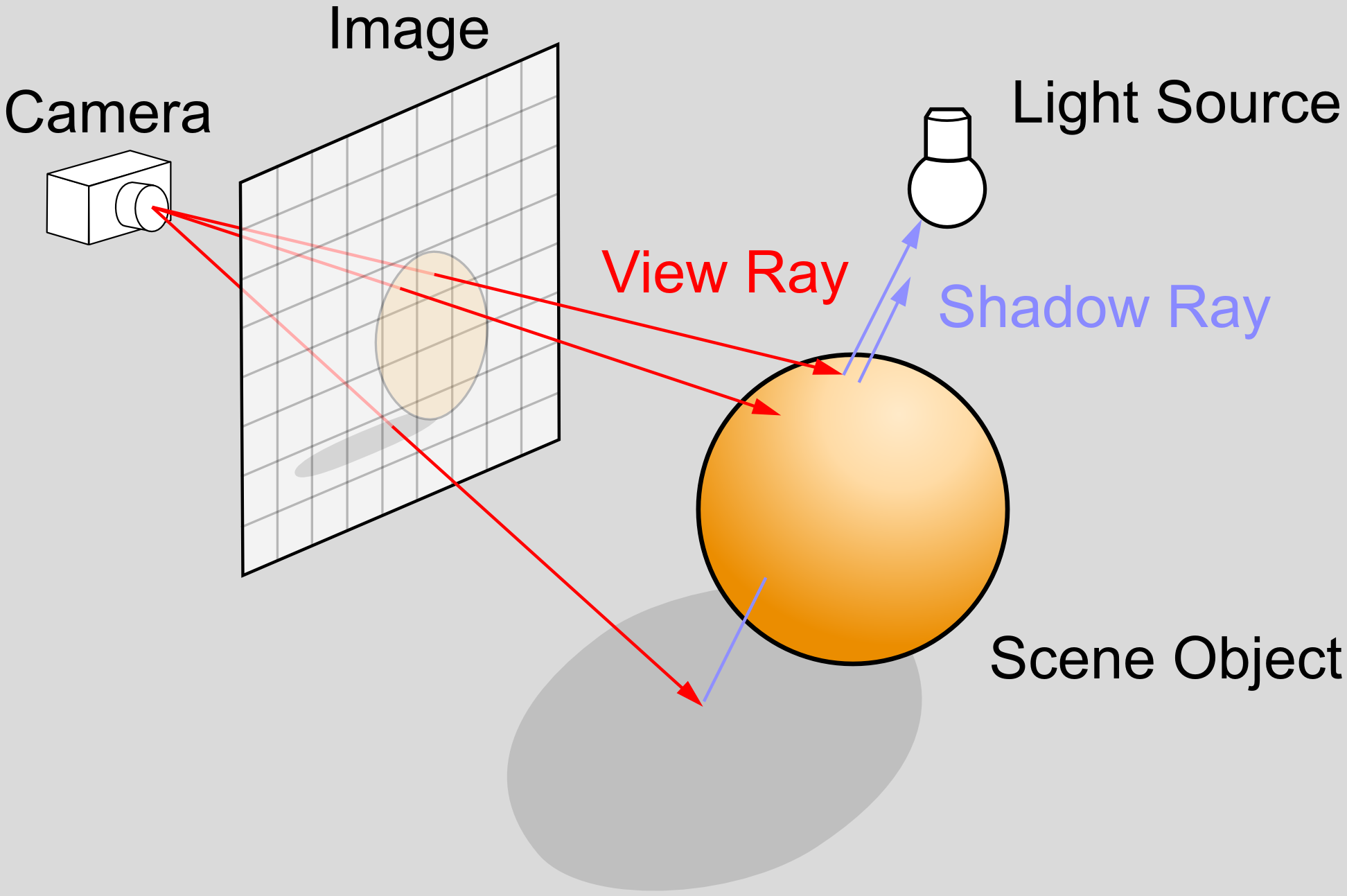 [ henrik link ]
|
|
modeling quality \(\quad\Rightarrow\quad\) render quality (light source, camera, materials, surfaces) |
|
modeling light sources is relatively easy  [ paul debevec link ]
|
 |
 |
|
modeling camera lens system can be complex 
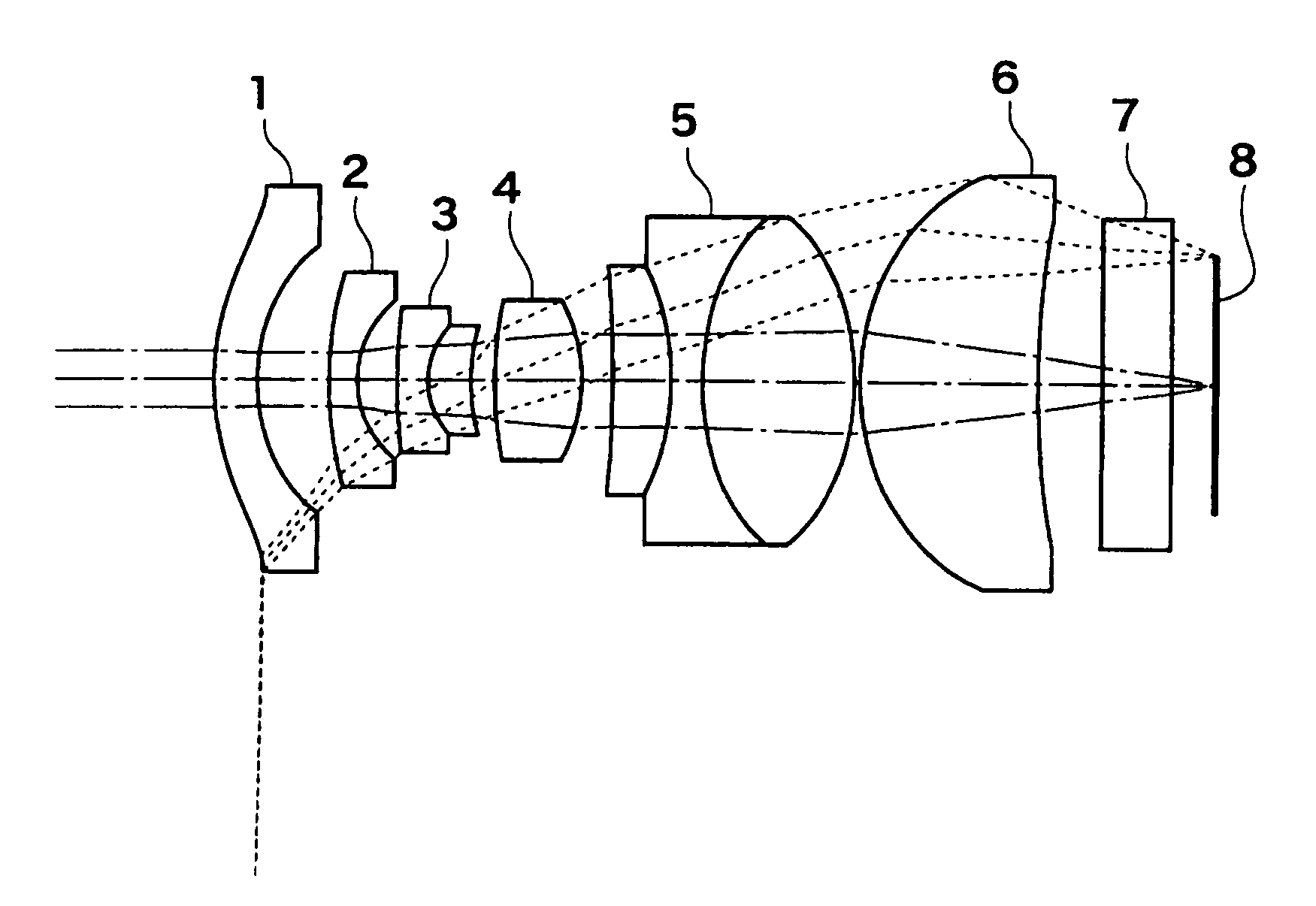 |
|
pinhole works surprisingly well, much easier to control 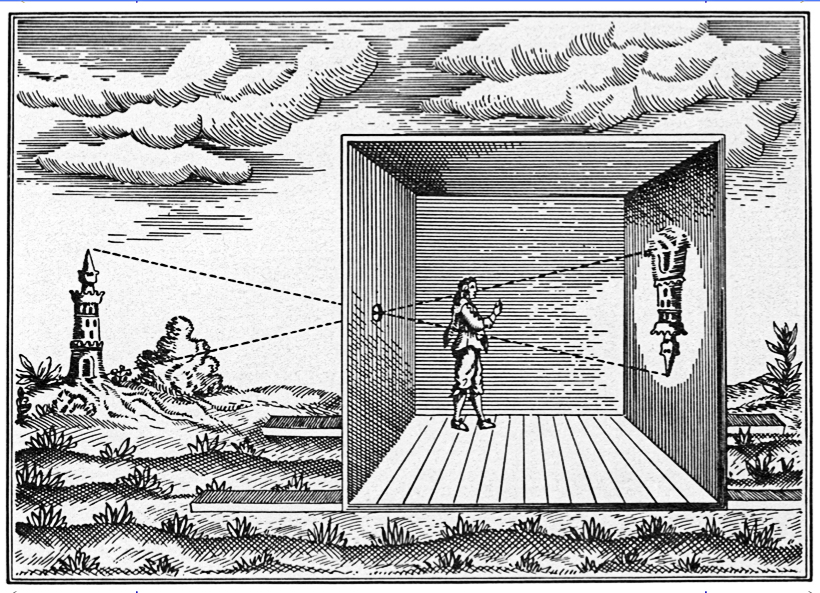
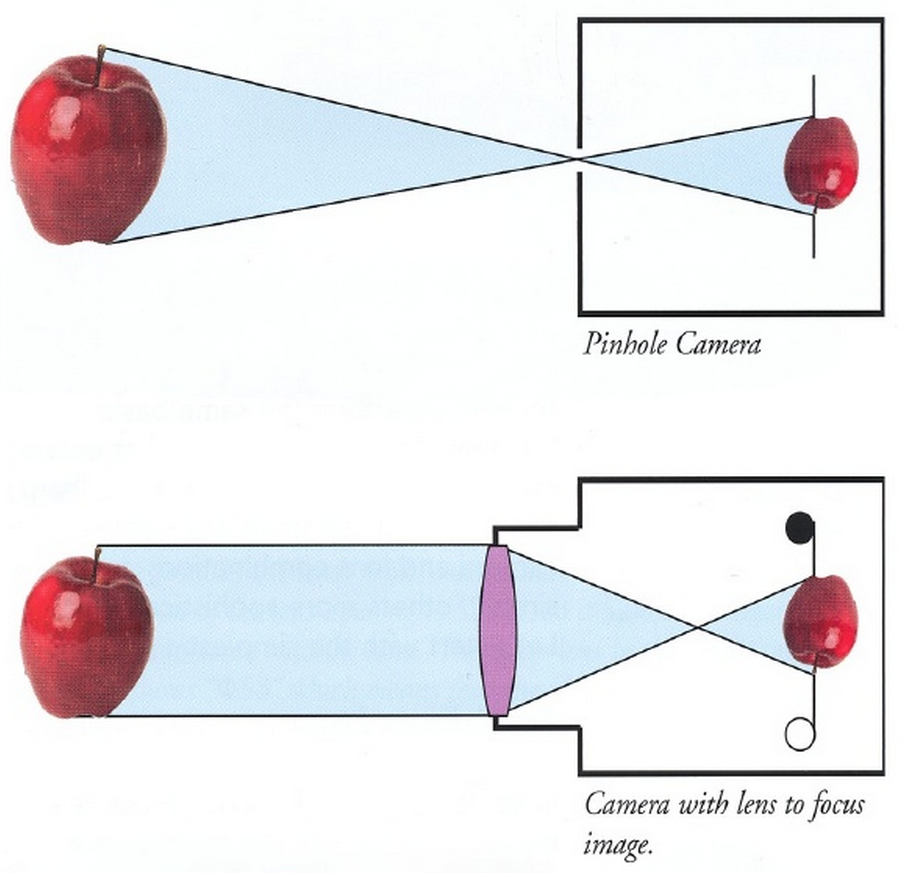 |
|
modeling materials is not difficult  [ marc tardif link ]
|
|
light reflects off surface in all directions at different amounts materials describe how much light bounces  [ andrey s. lebedev link ]
|
|
we can faithfully describe almost any material as a |
|
\[\begin{array}{ll} \text{diffuse} & \rho(...) = \frac{\red R_d}{\pi} \\ \text{specular} & \rho(...) = {\red R_s} (\mathbf{h} \cdot \mathbf{n})^{\red p} \\ \end{array}\] 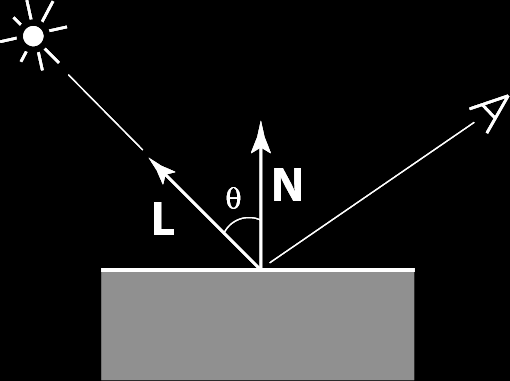
 |
|
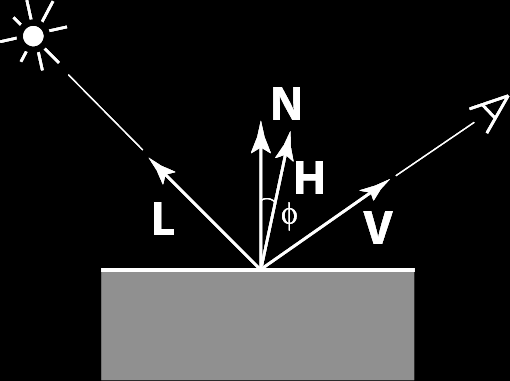
\[\begin{array}{rcl} \rho(...) & = & a \cdot b \cdot F(\omega_i \cdot \mathbf{h}) \\ a & = & \frac{\sqrt{({\red n_u}+1)({\red n_v}+1)}}{8\pi} \\ b & = & \frac{(\mathbf{n}\cdot\mathbf{h})^{{\red n_u}\cos^2\phi+{\red n_v}\sin^2\phi}}{(\mathbf{h}\cdot\omega_i)\max(\cos\theta_i,\cos\theta_o)} \\ F(\omega_i \cdot \mathbf{h}) & = & {\red R_s} + (1-{\red R_s})(1-(\omega_i \cdot \mathbf{h}))^5 \end{array}\] (schlick's approximation to the fresnel equation) |
 [ jensen ]
|
 [ jensen ]
|
 [ debevec, link ]
|
|
modeling surfaces is straightforward  |
|
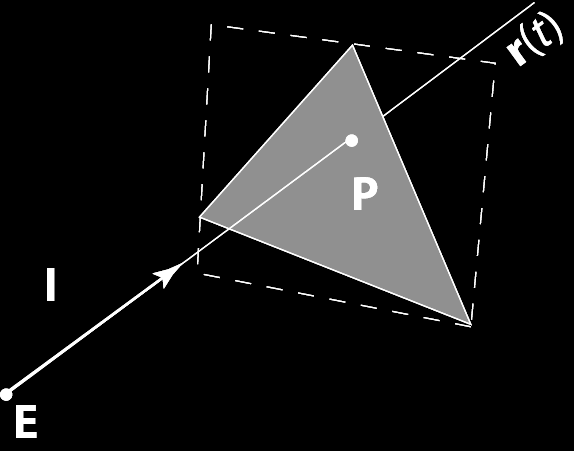
use triangles to describe any surface to arbitrary precision |
|
using ray for light and triangle for surface, \[\begin{array}{ll} \text{ray} & P = P_o + tV \\ \text{plane} & P \cdot N + d = 0 \\ \text{ray-plane} & t = -(P_o \cdot N + d) / (V \cdot N) \\ \end{array}\] 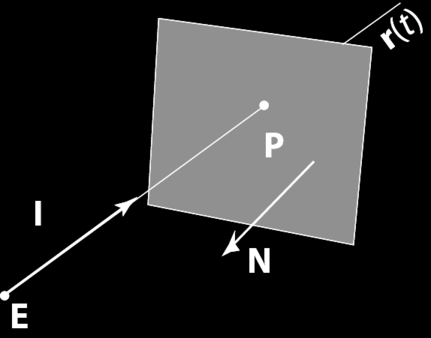
 |
|
the rendering equation puts the parts together all photo-realistic graphics engines solve this equation |
|
\[L_o (\mathbf{x}, \omega_o) = L_e(\mathbf{x}, \omega_o) + \int_\Omega \rho(\mathbf{x}, \omega_i, \omega_o) L_i(\mathbf{x}, \omega_i) (\omega_i \cdot \mathbf{n}) d\omega_i\] emit (\(L_e\)), camera (\(L_o\)), bounce (\(\rho\), \(L_i\), \(L_o\)) |
|
the only thing remaining is doing the light simulation solve the rendering equation |
|
"what do we do now sheriff?" "now, we render" |
the bad
|
light simulation isn't cheap steps toward photo-realism causes computation time to grow |
|
for example, let's look at rendering an image note: following simulations are already "smart" |
 simple |
 shadows |
 mirror reflection |
 soft shadows |
 multiple bounces |
 glossy reflection |
 translucency |
 environment |
|
and it only gets worse from here |
|
adding more realism involves computing more light bounces |
the weird
|
we could use approximations for the rendering equation |
|
the following are a few different ways |
|
put triangles into boxes  |
|
throw darts 

 |
|
roll multiple unfair dice 
 [ merity et al. link ]
|
the end
|
[ the third and the seventh, by alex roman link ]
|
|
[ eye piece, by chris jones link ]
|
|
[ snappers facial rig, by snappers mocap link ]
|
|
[ roundtrip, by david gruwier link ]
|
|
[ light stage, hawkins et al. link ]
|