Stereo Matching

COS 351 - Computer Vision

Fundamental Matrix

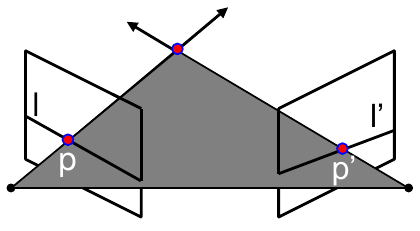
Let \(p\) be a point in left image, \(p'\) in right image Epipolar relation \(p\) maps to epipolar line \(l'\) \(p'\) maps to epipolar line \(l\) Epipolar mapping described by a 3x3 matrix \(F\) \[l' = Fp \quad\quad l = p'F\] It follows that \[p'Fp = 0\]

Fundamental Matrix

This matrix \(F\) is called

• "Essential Matrix" when image intrinsic parameters are known
• "Fundamental Matrix" more generally (uncalibrated case)

Can solve for \(F\) from point correspondences

• Each \((p,p')\) pair gives one linear equation in entries of \(F\) \[p'Fp = 0\]
• \(F\) has 9 entries, but really only 7 or 8 degrees of freedom
• With 8 points, it is simple to solve for \(F\), but it is also possible with 7. See Marc Pollefey's notes for a nice tutorial.

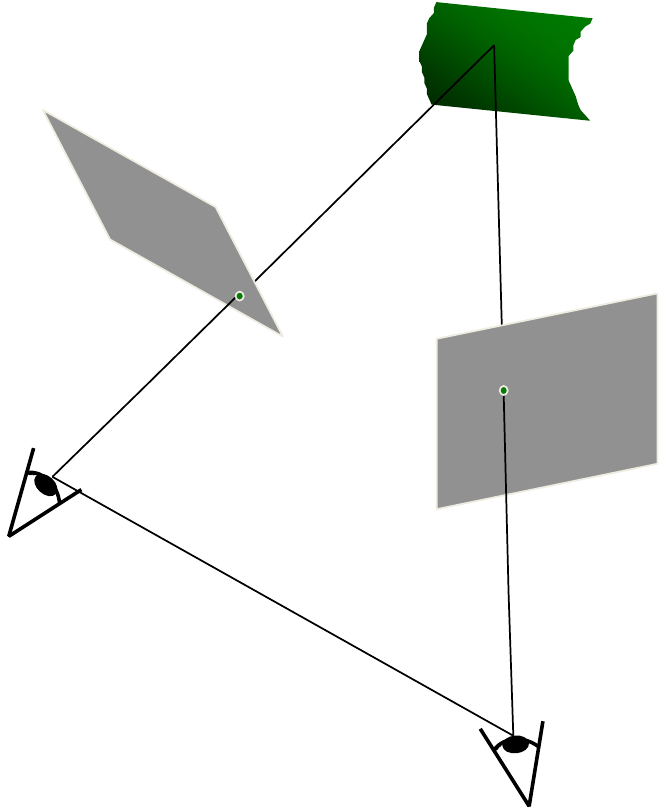
stereo image rectification

Reproject image planes onto a common plane parallel to the line between camera centers Pixel motion is horizontal after this transformation Two homographies (3x3 transform), one for each input image reprojection C.Loop and Z.Zhang. Computing Rectifying Homographies for Stereo Vision. IEEE Conf. Computer Vision and Pattern Recognition, 1999. link

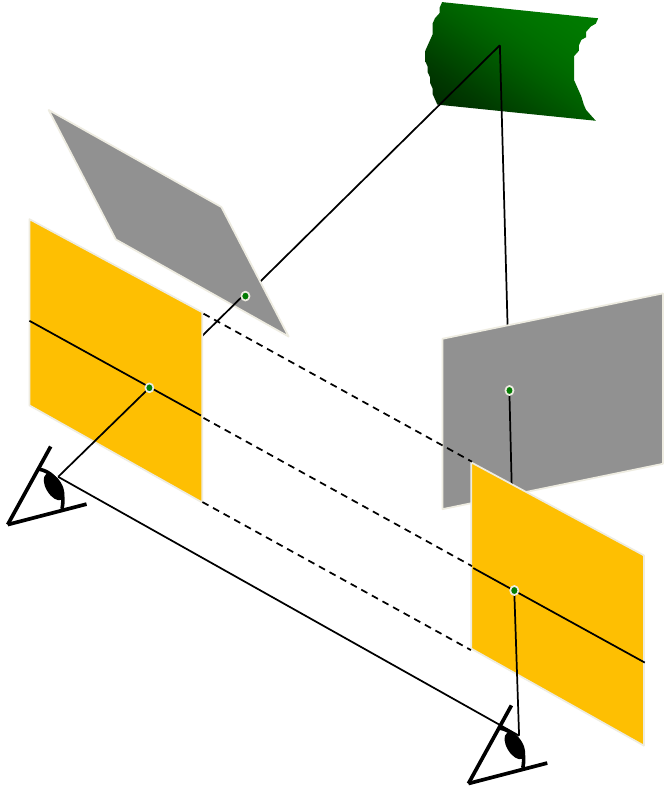rectification example

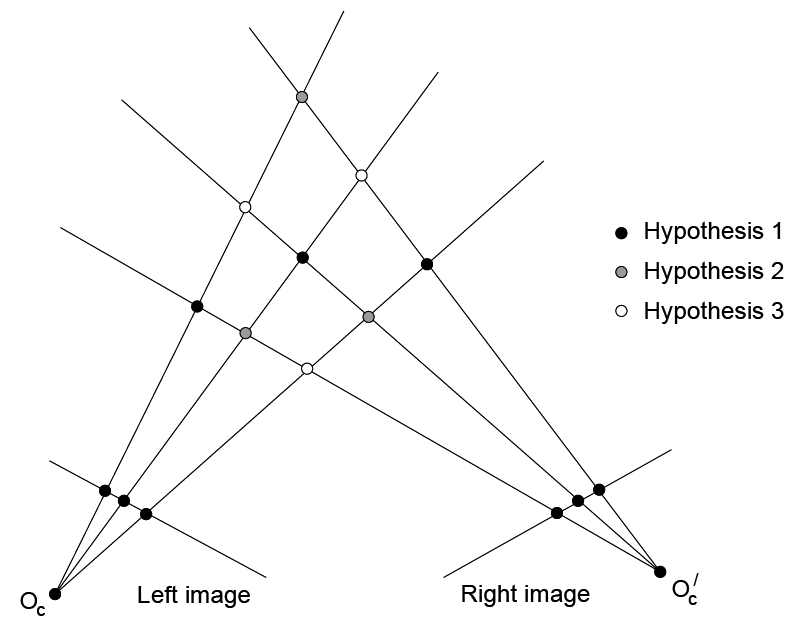
correspondence problem

Epipolar geometry constrains our search, but we still have a difficult correspondence problem.

correspondence problem

Multiple match hypotheses satisfy epipolar constraint, but which is correct?

correspondence problem

Beyond the hard constraint of epipolar geometry, there are "soft" constraints to help identify corresponding points

• similarities
• uniqueness
• ordering
• disparity gradient

To find matches in the image pair, we will assume

• most scene points visible from both views
• image regions for the matches are similar in appearance

dense correspondence search

• For each epipolar line
  • For each pixel/window in left image
    • Compare with every pixel/window on same epipolar line in right image
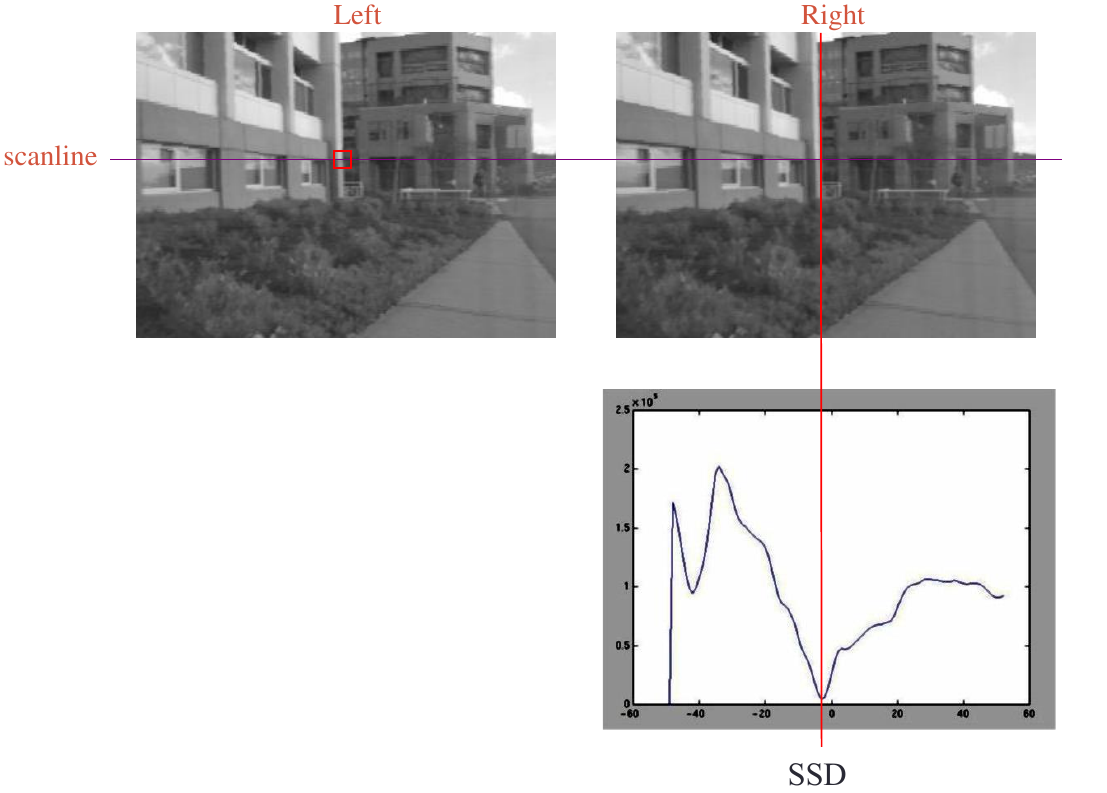
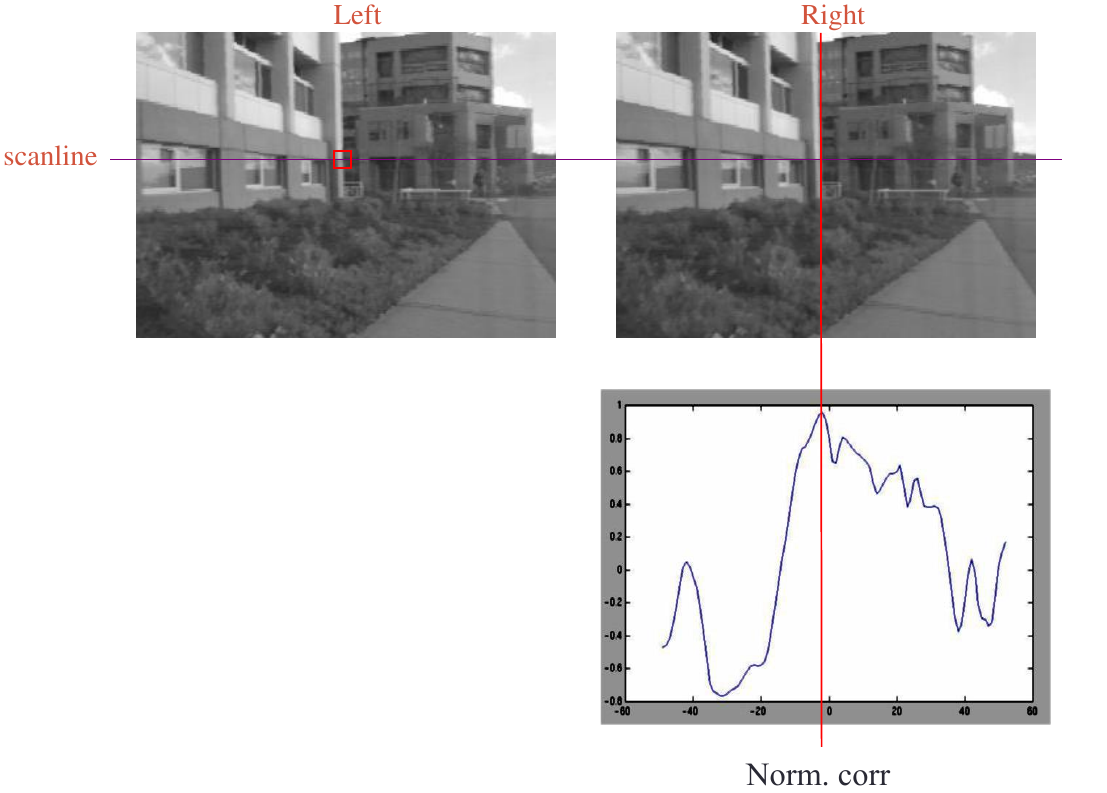
    • Pick position with minimum match cost (e.g., SSD, normalized correlation)

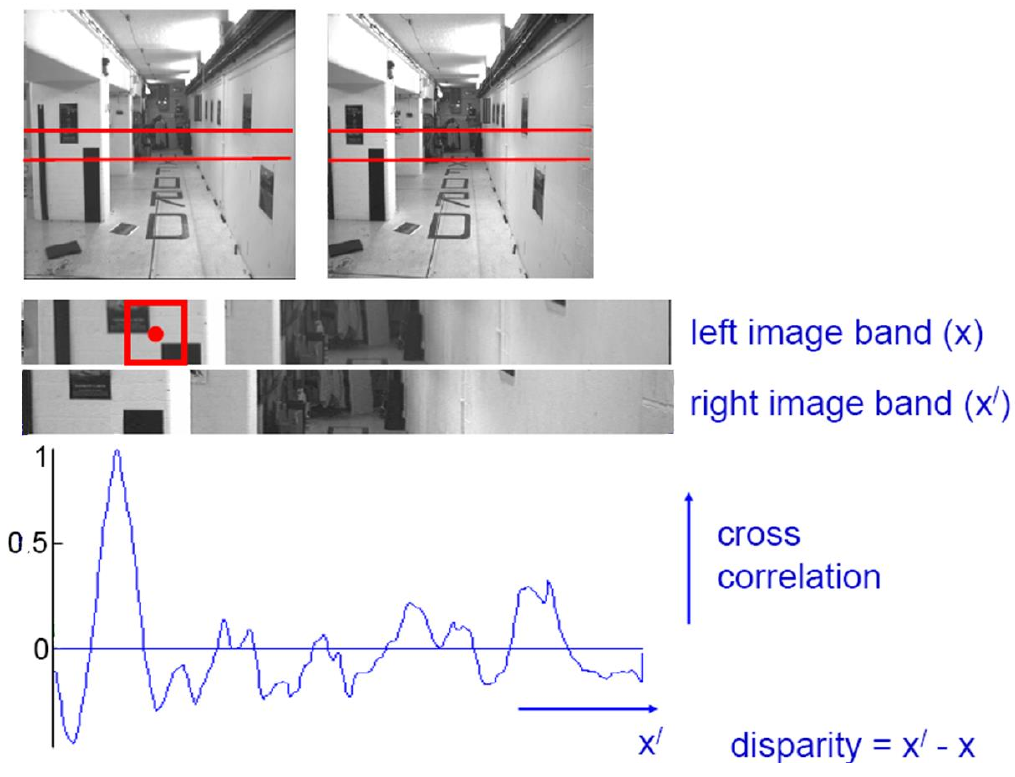
corr. search with similarity constraint

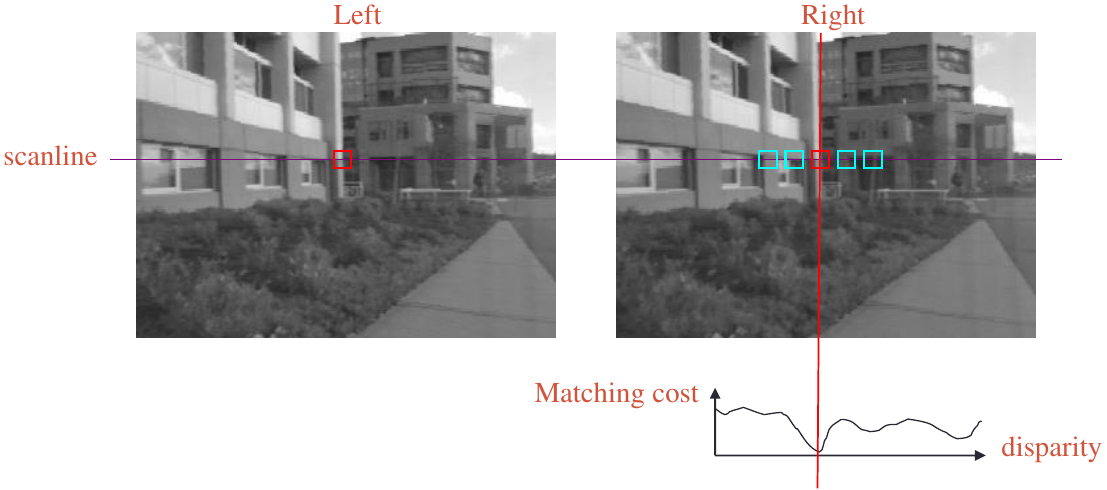
• Slide a window along the right scanline and compare contents of that window with the reference window in the left image
• Matching cost: SSD or normalized correlation

corr. search with similarity constraint

corr. search with similarity constraint

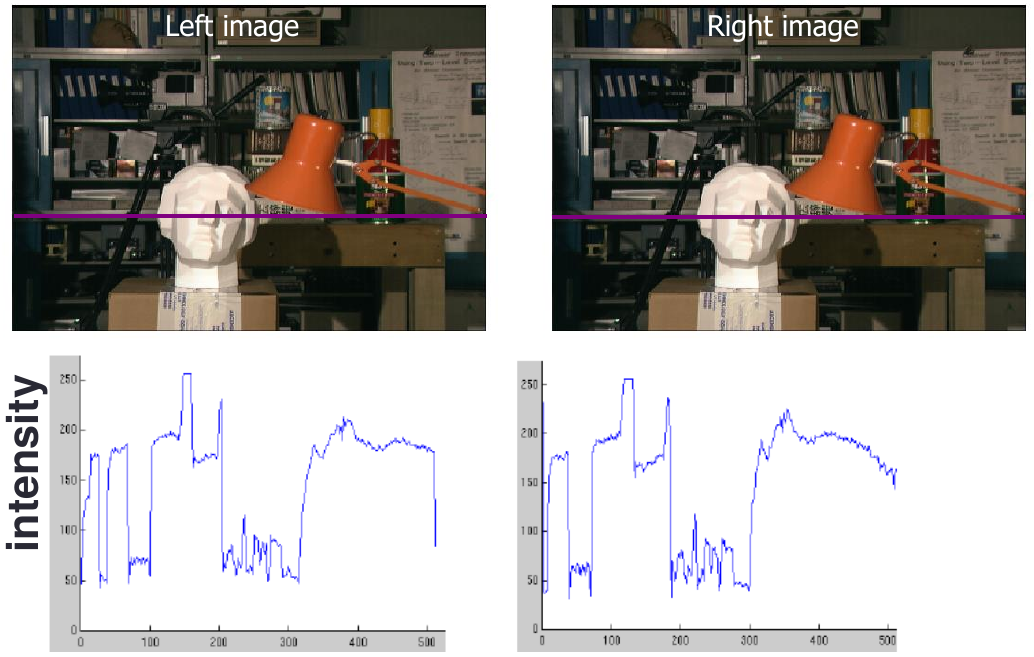
correspondence problem

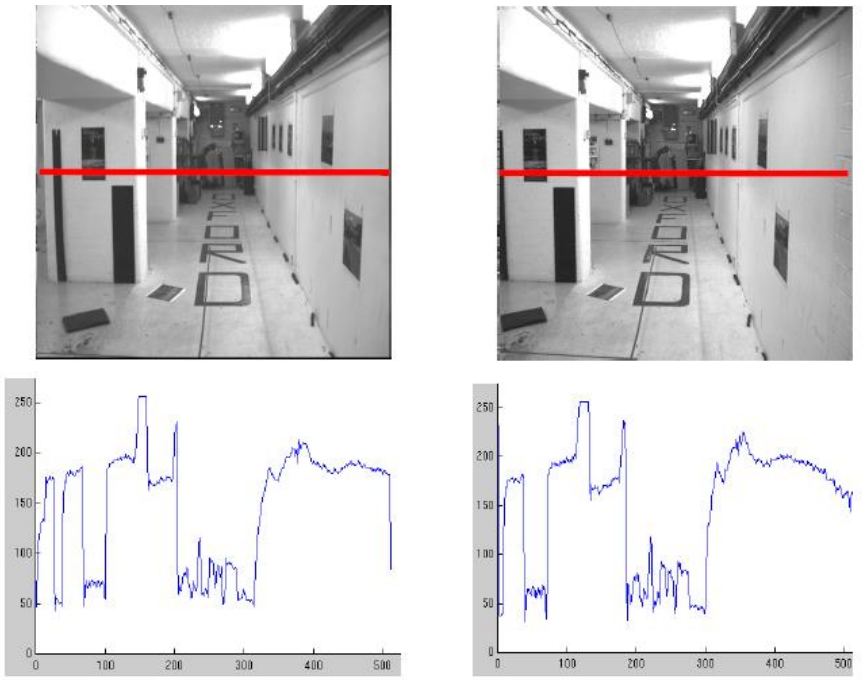
Clear correspondence between intensities, but also noise and ambiguity

correspondence problem

Neighborhoods of corresponding points are similar in intensity patterns

correspondence problem

correspondence problem

correspondence problem

correspondence problem

correspondence problem

effect of window size

effect of window size

Want window large enough to have sufficient intensity variation, yet small enough to contain only pixels with about the same disparity.

results with window search

better solutions

• Beyond individual correspondences to estimate disparities
• Optimize correspondences assignments jointly
  • Scanline at a time (dynamic programming)
  • Full 2D grid (graph cuts)

scanline stereo

• Try to coherently match pixels on the entire scanline
• Different scanlines are still optimized independently

coherent stereo on 2D grid

• Scanline stereo generates streaking artifacts

• Can't use dynamic programming to find spatially coherent disparities/correspondences on a 2D grid

stereo as energy minimization

• What defines a good stereo correspondence?
  1. Match quality
     • Want each pixel to find a good match in the other image
  2. Smoothness
     • If two pixels are adjacent, they should (usually) move about the same amount

stereo as energy minimization

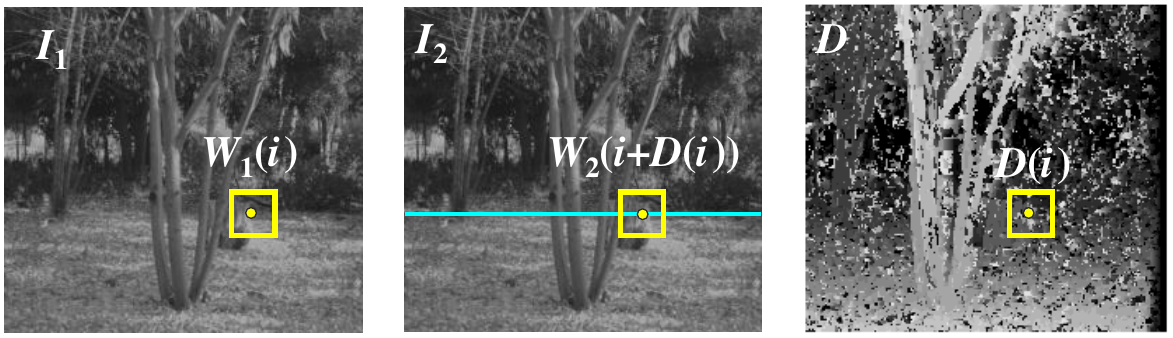
\[\begin{array}{cc} E = \alpha E_\text{data}(I_1,I_2,D)+ \beta E_\text{smooth}(D) & \begin{array}{c} E_\text{data} = \sum_i \bigl(W_1(i) - W_2(i+D(i))\bigr)^2 \\ E_\text{smooth} = \sum_{\mathrm{neighbors}\ i,j} \rho\bigl(D(i) - D(j)\bigr) \end{array}\end{array}\]

Energy functions of this form can be minimized using graph cuts

Y.Boykov, O.Veksler, and R.Zabih. Fast Approximate Energy Minimization via Graph Cuts. PAMI 2001. link

stereo as energy minimization

Better results!

For the latest and greatest: http://vision.middlebury.edu/stereo/

challenges

• Low-contrast; texture-less image regions
• Occlusions
• Violations of brightness constancy (e.g., specular reflections)
• Really large baselines (foreshortening and appearance change)
• Camera calibration errors

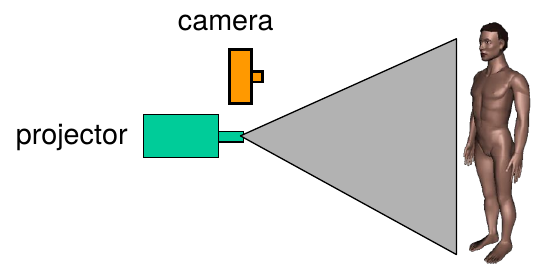
active stereo with structured light

Project "structured" light patterns onto the object

Simplifies the correspondence problem Allows us to use only one camera

L.Zhang, B.Curless, and S.M.Seitz. Rapid Shape Acquisition Using Color Structured Light and Multi-pass Dynamic Programming. 3DPVT 2002. link

Kinect: Structured infared light

https://bbzippo.wordpress.com/2010/11/28/kinect-in-infrared/

summary

• Epipolar geometry
  • Epipoles are intersection of baseline with image planes
  • Matching point in second image is on a line passing through its epipole
  • Fundamental matrix maps from a point in one image to a line (its epipolar line) in the other
  • Can solve for \(F\) given corresponding points (e.g., interest points)
• Stereo depth estimation
  • Estimate disparity by finding corresponding points along scanlines
  • Depth is inverse to disparity