
Camera Calibration
COS 351 - Computer Vision
depth from disparity
So if we could find the corresponding points in two images, we could estimate relative depth...



\[(x',y') = (x+D(x,y), y)\]
what did we need to know?
- Correspondence for every pixel. Sort of like assign02, but assign02 is "sparse" and we need "dense" correspondence
- Calibration for the cameras

where do we need to search?

where do we need to search?

where do we need to search?


how do we calibrate a camera?

how do we calibrate a camera?

world vs. camera coordinates

projection: world coords -> image coords
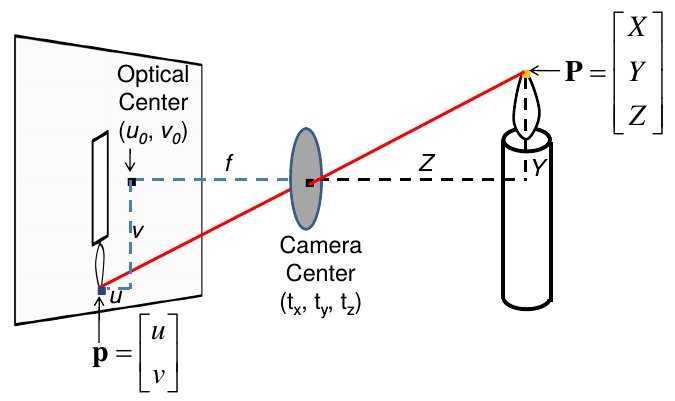
homogeneous coordinates
Converting between coordinates spaces
\[ \begin{array}{cc} \text{image coords} & \text{scene coords} \\ (x,y) \Rightarrow \left[ \begin{array}{c} x \\ y \\ 1 \end{array} \right] & (x,y,z) \Rightarrow \left[ \begin{array}{c} x \\ y \\ z \\ 1 \end{array} \right] \\ \left[ \begin{array}{c} x \\ y \\ w \end{array} \right] \Rightarrow (x/w, y/w) & \left[ \begin{array}{c} x \\ y \\ z \\ w \end{array} \right] \Rightarrow (x/w, y/w, z/w) \\ \end{array} \]
projection matrix
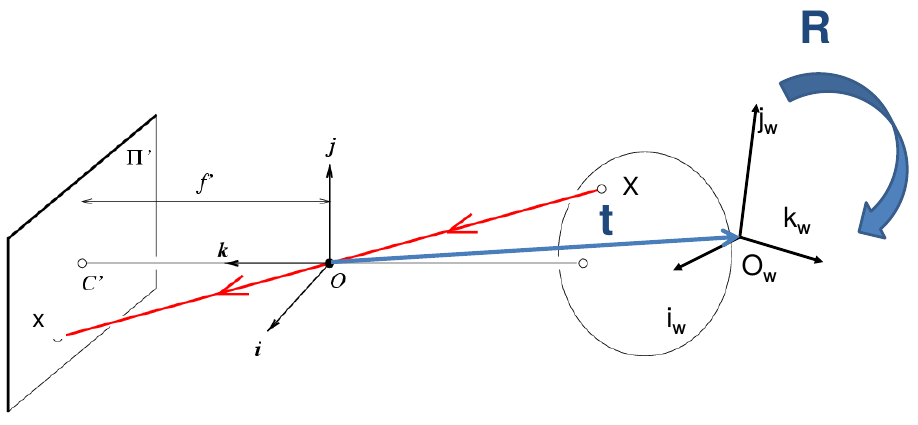
\[\mathbf{x} = \mathbf{K}[\mathbf{R}\ \mathbf{t}]\mathbf{X}\]
\[\begin{array}{cl} \mathbf{x} & \text{image coords }(u,v,1) \\ \mathbf{K} & \text{intrinsic matrix (3x3)} \\ \mathbf{R} & \text{rotation matrix (3x3)} \\ \mathbf{t} & \text{translation matrix (3x1)} \\ \mathbf{X} & \text{world coords }(X,Y,Z,1) \end{array}\]
projection matrix
\[ \mathbf{x} = \mathbf{K}[\mathbf{I}\ \mathbf{0}]\mathbf{X} \Rightarrow w\left[\begin{array}{c}u \\ v \\ 1\end{array}\right] = \left[\begin{array}{ccc} f & 0 & 0 \\ 0 & f & 0 \\ 0 & 0 & 1 \end{array}\right] \left[\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array}\right] \left[\begin{array}{c} x \\ y \\ z \\ 1 \end{array}\right] \]
|
Intrinsic assumptions
|
Extrinsic assumptions
|
projection matrix
\[ \mathbf{x} = \mathbf{K}[\mathbf{I}\ \mathbf{0}]\mathbf{X} \Rightarrow w\left[\begin{array}{c}u \\ v \\ 1\end{array}\right] = \left[\begin{array}{ccc} f & 0 & u_0 \\ 0 & f & v_0 \\ 0 & 0 & 1 \end{array}\right] \left[\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array}\right] \left[\begin{array}{c} x \\ y \\ z \\ 1 \end{array}\right] \]
|
Intrinsic assumptions
|
Extrinsic assumptions
|
projection matrix
\[ \mathbf{x} = \mathbf{K}[\mathbf{I}\ \mathbf{0}]\mathbf{X} \Rightarrow w\left[\begin{array}{c}u \\ v \\ 1\end{array}\right] = \left[\begin{array}{ccc} \alpha & 0 & u_0 \\ 0 & \beta & v_0 \\ 0 & 0 & 1 \end{array}\right] \left[\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array}\right] \left[\begin{array}{c} x \\ y \\ z \\ 1 \end{array}\right] \]
|
Intrinsic assumptions
|
Extrinsic assumptions
|
projection matrix
\[ \mathbf{x} = \mathbf{K}[\mathbf{I}\ \mathbf{0}]\mathbf{X} \Rightarrow w\left[\begin{array}{c}u \\ v \\ 1\end{array}\right] = \left[\begin{array}{ccc} \alpha & s & u_0 \\ 0 & \beta & v_0 \\ 0 & 0 & 1 \end{array}\right] \left[\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array}\right] \left[\begin{array}{c} x \\ y \\ z \\ 1 \end{array}\right] \]
|
Intrinsic assumptions
|
Extrinsic assumptions
|
oriented and translated camera

projection matrix
\[ \mathbf{x} = \mathbf{K}[\mathbf{I}\ \mathbf{t}]\mathbf{X} \Rightarrow w\left[\begin{array}{c}u \\ v \\ 1\end{array}\right] = \mathbf{K} \left[\begin{array}{cccc} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \end{array}\right] \left[\begin{array}{c} x \\ y \\ z \\ 1 \end{array}\right] \]
|
Intrinsic assumptions
|
Extrinsic assumptions
|
3d rotation of points
Rotation around the coordinate axes, counter-clockwise:
|
|
\[ R_x(\theta) = \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{array}\right] \] \[ R_y(\phi) = \left[\begin{array}{ccc} \cos\phi & 0 & \sin\phi \\ 0 & 1 & 0 \\ -\sin\phi & 0 & \cos\phi \end{array}\right] \] \[ R_z(\psi) = \left[\begin{array}{ccc} \cos\psi & -\sin\psi & 0 \\ \sin\psi & \cos\psi & 0 \\ 0 & 0 & 1 \end{array}\right] \] |
projection matrix
\[ \mathbf{x} = \mathbf{K}[\mathbf{R}\ \mathbf{t}]\mathbf{X} \Rightarrow w\left[\begin{array}{c}u \\ v \\ 1\end{array}\right] = \mathbf{K} \left[\begin{array}{cccc} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \end{array}\right] \left[\begin{array}{c} x \\ y \\ z \\ 1 \end{array}\right] \]
|
Intrinsic assumptions
|
Extrinsic assumptions
|
degrees of freedom
\[ \mathbf{x} = \mathbf{K} \left[\begin{array}{cc}\mathbf{R} & \mathbf{t} \end{array}\right] \mathbf{X} \]
\[ w\left[\begin{array}{c}u \\ v \\ 1\end{array}\right] = \left[\begin{array}{ccc} \alpha & s & u_0 \\ 0 & \beta & v_0 \\ 0 & 0 & 1 \end{array}\right] \left[\begin{array}{cccc} r_{11} & r_{12} & r_{13} & t_x \\ r_{21} & r_{22} & r_{23} & t_y \\ r_{31} & r_{32} & r_{33} & t_z \end{array}\right] \left[\begin{array}{c} x \\ y \\ z \\ 1 \end{array}\right] \]
- \(\mathbf{K}\) : 5 (\(\alpha\), \(s\), \(u_0\), \(\beta\), \(v_0\))
- \([\mathbf{R\ t}]\) : 6 (\(\theta\), \(\phi\), \(\psi\), \(t_x\), \(t_y\), \(t_z\))
beyond pinholes: radial distortion
- Common in wide-angle lenses or for special applications (e.g., security)
- Creates non-linear terms in projection
- Usually handled by solving for non-linear terms and then correcting image
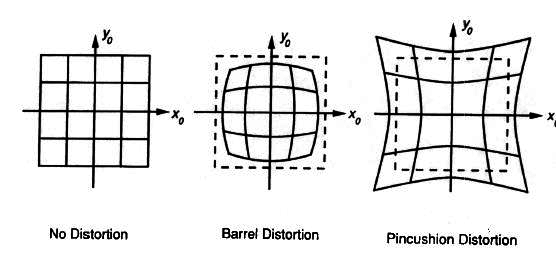

how to calibrate the camera
\[ \mathbf{x} = \mathbf{K} \left[\begin{array}{cc}\mathbf{R} & \mathbf{t} \end{array}\right] \mathbf{X} \]
\[ \left[\begin{array}{c} su \\ sv \\ s \end{array}\right] = \left[\begin{array}{cccc}* & * & * & * \\ * & * & * & * \\ * & * & * & * \end{array}\right] \left[\begin{array}{c} X \\ Y \\ Z \\ 1 \end{array}\right] \]
calibrating the camera
Use a scene with known geometry
- Correspond image points to 3D points
- Get least squares solution (or non-linear solution)

\[\left[\begin{array}{c} su \\ sv \\ s \end{array}\right] = \left[\begin{array}{cccc} m_{11} & m_{12} & m_{13} & m_{14} \\ m_{21} & m_{22} & m_{23} & m_{24} \\ m_{31} & m_{32} & m_{33} & m_{34} \end{array}\right] \left[\begin{array}{C} X \\ Y \\ Z \\ 1 \end{array}\right]\]
how do we calibrate a camera?

method 1: homogeneous linear system
\[\left[\begin{array}{c} su \\ sv \\ s \end{array}\right] = \left[\begin{array}{cccc} m_{11} & m_{12} & m_{13} & m_{14} \\ m_{21} & m_{22} & m_{23} & m_{24} \\ m_{31} & m_{32} & m_{33} & m_{34} \end{array}\right] \left[\begin{array}{C} X \\ Y \\ Z \\ 1 \end{array}\right]\]
Solve for \(m\)'s entries using linear least squares (\(\mathbf{A}\mathbf{x} = \mathbf{0}\) form)
\[\left[\begin{array}{cccccccccccc} X_1 & Y_1 & Z_1 & 1 & 0 & 0 & 0 & 0 & -u_1X_1 & -u_1Y_1 & -u_1Z_1 & -u_1 \\ 0 & 0 & 0 & 0 & X_1 & Y_1 & Z_1 & 1 & -v_1X_1 & -v_1Y_1 & -v_1Z_1 & -v_1 \\ & & & & & & \vdots & & & & & & \\ X_n & Y_n & Z_n & 1 & 0 & 0 & 0 & 0 & -u_nX_n & -u_nY_n & -u_nZ_n & -u_n \\ 0 & 0 & 0 & 0 & X_n & Y_n & Z_n & 1 & -v_nX_n & -v_nY_n & -v_nZ_n & -v_n \end{array}\right] \left[\begin{array}{c} m_{11} \\ m_{12} \\ m_{13} \\ m_{14} \\ m_{21} \\ m_{22} \\ m_{23} \\ m_{24} \\ m_{31} \\ m_{32} \\ m_{33} \\ m_{34} \end{array}\right] = \left[\begin{array}{c} 0 \\ 0 \\ \vdots \\ 0 \\ 0 \end{array}\right] \]
[U,S,V] = svd(A); M = V(:,end); M = reshape(M,[],3)';
method 2: nonhomogeneous linear system
\[\left[\begin{array}{c} su \\ sv \\ s \end{array}\right] = \left[\begin{array}{cccc} m_{11} & m_{12} & m_{13} & m_{14} \\ m_{21} & m_{22} & m_{23} & m_{24} \\ m_{31} & m_{32} & m_{33} & 1 \end{array}\right] \left[\begin{array}{C} X \\ Y \\ Z \\ 1 \end{array}\right]\]
Solve for \(m\)'s entries using linear least squares (\(\mathbf{A}\mathbf{x} = \mathbf{b}\) form)
\[\left[\begin{array}{ccccccccccc} X_1 & Y_1 & Z_1 & 1 & 0 & 0 & 0 & 0 & -u_1X_1 & -u_1Y_1 & -u_1Z_1 \\ 0 & 0 & 0 & 0 & X_1 & Y_1 & Z_1 & 1 & -v_1X_1 & -v_1Y_1 & -v_1Z_1 \\ & & & & & & \vdots & & & & & \\ X_n & Y_n & Z_n & 1 & 0 & 0 & 0 & 0 & -u_nX_n & -u_nY_n & -u_nZ_n \\ 0 & 0 & 0 & 0 & X_n & Y_n & Z_n & 1 & -v_nX_n & -v_nY_n & -v_nZ_n \end{array}\right] \left[\begin{array}{c} m_{11} \\ m_{12} \\ m_{13} \\ m_{14} \\ m_{21} \\ m_{22} \\ m_{23} \\ m_{24} \\ m_{31} \\ m_{32} \\ m_{33} \end{array}\right] = \left[\begin{array}{c} u_1 \\ v_1 \\ \vdots \\ u_n \\ v_n \end{array}\right] \]
M = A \ Y; M = [M;1]; M = reshape(M,[],3)';
calibration with linear method
- Advantages
- Easy to formulate and solve
- Provides initialization for non-linear methods
- Disadvantages
- Doesn't directly give you camera parameters
- Doesn't model radial distortion
- Can't impose constraints, such as known focal length
- Non-linear methods are preferred
- Define error as difference between projected points and measured points
- Minimize error using Newton's method or other non-linear optimization
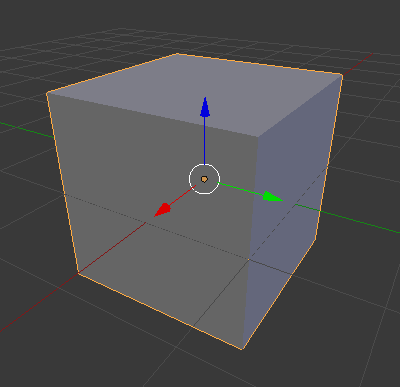 \(R_x(0^\circ)\)
\(R_x(0^\circ)\) \(R_x(15^\circ)\)
\(R_x(15^\circ)\) \(R_x(30^\circ)\)
\(R_x(30^\circ)\) 