Lights and Materials

COS 350 - Computer Graphics

Lighting the scene

Lighting the scene

Naïve approach is to assign to each vertex a color that seems as though it is lit.

Does not work if we transform the light, the object, or the camera!

Model lights and materials

definition (non-technical)

Materials

the surface characteristics that describe how the light is reflected, absorbed, transmitted, scattered, emitted, etc., off/at the surface.

light model

Light properties:

light model

Light properties:

• position
• orientation
• color + brightness
• type (point, spot, directional, etc.)
  • properties of type

material model

Material properties:

material model

Material properties:

• color (diffuseness)
• shininess (reflectiveness/specularity)
• translucency (transmittance)
• subsurface scattering
• emittance

geometry model

Geometry properties:

geometry model

Geometry properties:

• position
• orientation (normal, tangents)

simplified model

For now, we will only consider a small subset of these properties:

• Light (directional)
  • orientation
  • color + brightness
  • type: directional
• Material
  • diffuse color
• Geometry
  • normal

simplified model

simplified light

Directional light has no position, only an orientation.

Define this as a direction (unit vector)

Specified in shader using uniform vec3, because the direction will not change for each fragment.

simplified light

Similarly, the color and brightness can be specified in shader as uniform vec3.

simplified material + geometry

The intensity of light that is reflected into the camera by the material of the surface depends on:

• the reflectiveness of the material
• the orientation of the surface relative to the light's orientation

simplified material + geometry

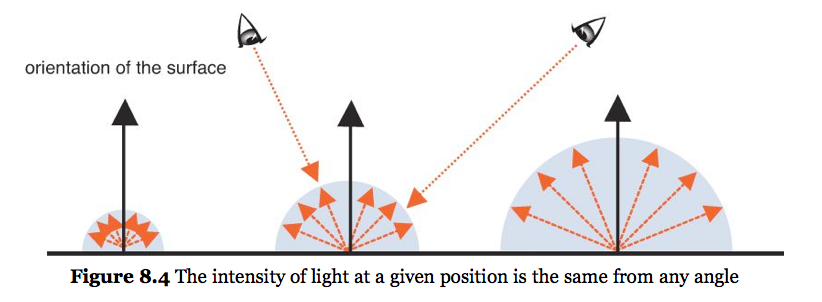
Diffuse materials scatter incident light equally in all directions, independent of the camera's orientation to the surface. (e.g., moon)

simplified material + geometry

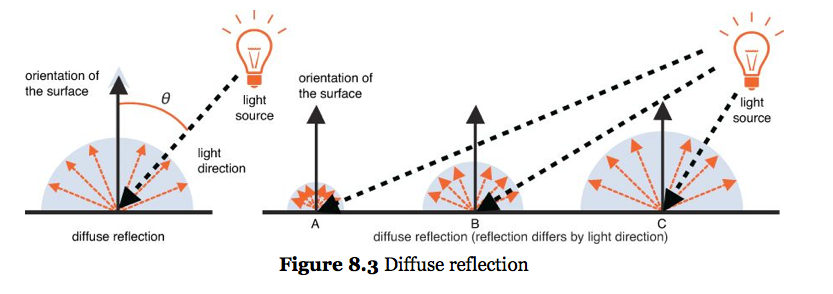
The intensity of reflected light does depend on the relative orientation of the surface to the light source. In other words, as the surface "turns away" from the light, the intensity of reflected light falls off.

simplified material + geometry

This fall-off can be computed as \(\cos(\theta)\), the cosine of the angle between the surface normal (\(\n\)) and the lighting direction (\(\l\)). Another mathematically equivalent way: \(\n \cdot \l\)

definition

normal

the direction that points "outside" the surface and is perpendicular to all tangent directions of the surface

lighted cube (animated)

lighted cube (animated)

// LightedCube_animation.js (c) 2012 matsuda
// Vertex shader program
var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'attribute vec4 a_Color;\n' +
  'attribute vec4 a_Normal;\n' +
  'uniform mat4 u_MvpMatrix;\n' +
  'uniform mat4 u_NormalMatrix;\n' +
  'uniform vec3 u_LightDirection;\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_Position = u_MvpMatrix * a_Position;\n' +
  '  vec4 normal = u_NormalMatrix * a_Normal;\n' +
  '  float nDotL = max(dot(u_LightDirection, normalize(normal.xyz)), 0.0);\n' +
  '  v_Color = vec4(a_Color.xyz * nDotL, a_Color.a);\n' + 
  '}\n';

// Fragment shader program
var FSHADER_SOURCE =
  '#ifdef GL_ES\n' +
  'precision mediump float;\n' +
  '#endif\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_FragColor = v_Color;\n' +
  '}\n';

function main() {
  // Retrieve <canvas> element
  var canvas = document.getElementById('webgl');

  // Get the rendering context for WebGL
  var gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('Failed to get the rendering context for WebGL');
    return;
  }

  // Initialize shaders
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to initialize shaders');
    return;
  }

  // 
  var n = initVertexBuffers(gl);
  if (n < 0) {
    console.log('Failed to set the vertex information');
    return;
  }

  // Set the clear color and enable the depth test
  gl.clearColor(0, 0, 0, 1);
  gl.enable(gl.DEPTH_TEST);

  // Get the storage locations of uniform variables and so on
  var u_MvpMatrix = gl.getUniformLocation(gl.program, 'u_MvpMatrix');
  var u_NormalMatrix = gl.getUniformLocation(gl.program, 'u_NormalMatrix');
  var u_LightDirection = gl.getUniformLocation(gl.program, 'u_LightDirection');
  if (!u_MvpMatrix || !u_NormalMatrix || !u_LightDirection) { 
    console.log('Failed to get the storage location');
    return;
  }

  var vpMatrix = new Matrix4();   // View projection matrix
  // Calculate the view projection matrix
  vpMatrix.setPerspective(30, canvas.width/canvas.height, 1, 100);
  vpMatrix.lookAt(3, 3, 7, 0, 0, 0, 0, 1, 0);
  // Set the light direction (in the world coordinate)
  var lightDirection = new Vector3([0.5, 3.0, 4.0]);
  lightDirection.normalize();     // Normalize
  gl.uniform3fv(u_LightDirection, lightDirection.elements);

  var currentAngle = 0.0;  // Current rotation angle
  var modelMatrix = new Matrix4();  // Model matrix
  var mvpMatrix = new Matrix4();    // Model view projection matrix
  var normalMatrix = new Matrix4(); // Transformation matrix for normals

  var tick = function() {
    currentAngle = animate(currentAngle);  // Update the rotation angle

    // Calculate the model matrix
    modelMatrix.setRotate(currentAngle, 0, 1, 0); // Rotate around the y-axis
    mvpMatrix.set(vpMatrix).multiply(modelMatrix);
    gl.uniformMatrix4fv(u_MvpMatrix, false, mvpMatrix.elements);

    // Pass the matrix to transform the normal based on the model matrix to u_NormalMatrix
    normalMatrix.setInverseOf(modelMatrix);
    normalMatrix.transpose();
    gl.uniformMatrix4fv(u_NormalMatrix, false, normalMatrix.elements);

    // Clear color and depth buffer
    gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);

    // Draw the cube
    gl.drawElements(gl.TRIANGLES, n, gl.UNSIGNED_BYTE, 0);

    requestAnimationFrame(tick, canvas); // Request that the browser ?calls tick
  };
  tick();
}

function draw(gl, n, angle, vpMatrix, u_MvpMatrix, u_NormalMatrix) {
}

function initVertexBuffers(gl) {
  // Create a cube
  //    v6----- v5
  //   /|      /|
  //  v1------v0|
  //  | |     | |
  //  | |v7---|-|v4
  //  |/      |/
  //  v2------v3
  // Coordinates
  var vertices = new Float32Array([
     1.0, 1.0, 1.0,  -1.0, 1.0, 1.0,  -1.0,-1.0, 1.0,   1.0,-1.0, 1.0, // v0-v1-v2-v3 front
     1.0, 1.0, 1.0,   1.0,-1.0, 1.0,   1.0,-1.0,-1.0,   1.0, 1.0,-1.0, // v0-v3-v4-v5 right
     1.0, 1.0, 1.0,   1.0, 1.0,-1.0,  -1.0, 1.0,-1.0,  -1.0, 1.0, 1.0, // v0-v5-v6-v1 up
    -1.0, 1.0, 1.0,  -1.0, 1.0,-1.0,  -1.0,-1.0,-1.0,  -1.0,-1.0, 1.0, // v1-v6-v7-v2 left
    -1.0,-1.0,-1.0,   1.0,-1.0,-1.0,   1.0,-1.0, 1.0,  -1.0,-1.0, 1.0, // v7-v4-v3-v2 down
     1.0,-1.0,-1.0,  -1.0,-1.0,-1.0,  -1.0, 1.0,-1.0,   1.0, 1.0,-1.0  // v4-v7-v6-v5 back
  ]);

  // Colors
  var colors = new Float32Array([
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0,     // v0-v1-v2-v3 front
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0,     // v0-v3-v4-v5 right
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0,     // v0-v5-v6-v1 up
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0,     // v1-v6-v7-v2 left
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0,     // v7-v4-v3-v2 down
    1, 0, 0,   1, 0, 0,   1, 0, 0,  1, 0, 0      // v4-v7-v6-v5 back
 ]);

  // Normal
  var normals = new Float32Array([
    0.0, 0.0, 1.0,   0.0, 0.0, 1.0,   0.0, 0.0, 1.0,   0.0, 0.0, 1.0,  // v0-v1-v2-v3 front
    1.0, 0.0, 0.0,   1.0, 0.0, 0.0,   1.0, 0.0, 0.0,   1.0, 0.0, 0.0,  // v0-v3-v4-v5 right
    0.0, 1.0, 0.0,   0.0, 1.0, 0.0,   0.0, 1.0, 0.0,   0.0, 1.0, 0.0,  // v0-v5-v6-v1 up
   -1.0, 0.0, 0.0,  -1.0, 0.0, 0.0,  -1.0, 0.0, 0.0,  -1.0, 0.0, 0.0,  // v1-v6-v7-v2 left
    0.0,-1.0, 0.0,   0.0,-1.0, 0.0,   0.0,-1.0, 0.0,   0.0,-1.0, 0.0,  // v7-v4-v3-v2 down
    0.0, 0.0,-1.0,   0.0, 0.0,-1.0,   0.0, 0.0,-1.0,   0.0, 0.0,-1.0   // v4-v7-v6-v5 back
  ]);

  // Indices of the vertices
  var indices = new Uint8Array([
     0, 1, 2,   0, 2, 3,    // front
     4, 5, 6,   4, 6, 7,    // right
     8, 9,10,   8,10,11,    // up
    12,13,14,  12,14,15,    // left
    16,17,18,  16,18,19,    // down
    20,21,22,  20,22,23     // back
 ]);

  // Write the vertex property to buffers (coordinates, colors and normals)
  if (!initArrayBuffer(gl, 'a_Position', vertices, 3, gl.FLOAT)) return -1;
  if (!initArrayBuffer(gl, 'a_Color', colors, 3, gl.FLOAT)) return -1;
  if (!initArrayBuffer(gl, 'a_Normal', normals, 3, gl.FLOAT)) return -1;

  // Unbind the buffer object
  gl.bindBuffer(gl.ARRAY_BUFFER, null);

  // Write the indices to the buffer object
  var indexBuffer = gl.createBuffer();
  if (!indexBuffer) {
    console.log('Failed to create the buffer object');
    return false;
  }
  gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER, indexBuffer);
  gl.bufferData(gl.ELEMENT_ARRAY_BUFFER, indices, gl.STATIC_DRAW);

  return indices.length;
}

function initArrayBuffer(gl, attribute, data, num, type) {
  // Create a buffer object
  var buffer = gl.createBuffer();
  if (!buffer) {
    console.log('Failed to create the buffer object');
    return false;
  }
  // Write date into the buffer object
  gl.bindBuffer(gl.ARRAY_BUFFER, buffer);
  gl.bufferData(gl.ARRAY_BUFFER, data, gl.STATIC_DRAW);
  // Assign the buffer object to the attribute variable
  var a_attribute = gl.getAttribLocation(gl.program, attribute);
  if (a_attribute < 0) {
    console.log('Failed to get the storage location of ' + attribute);
    return false;
  }
  gl.vertexAttribPointer(a_attribute, num, type, false, 0, 0);
  // Enable the assignment of the buffer object to the attribute variable
  gl.enableVertexAttribArray(a_attribute);

  return true;
}

// Rotation angle (degrees/second)
var ANGLE_STEP = 30.0;
// Last time that this function was called
var g_last = Date.now();
function animate(angle) {
  // Calculate the elapsed time
  var now = Date.now();
  var elapsed = now - g_last;
  g_last = now;
  // Update the current rotation angle (adjusted by the elapsed time)
  var newAngle = angle + (ANGLE_STEP * elapsed) / 1000.0;
  return newAngle %= 360;
}

link

transforming points, directions, normals

Transforming a point \(\x\) (vector) by the transformation matrix \(M\) is done by simple matrix-vector multiplication

\[M \x\]

Transforming a direction \(\d\) (unit vector) by the transformation matrix \(M\) is done by simple matrix-vector multiplication followed by a normalization (make result unit vector!)

\[\frac{M \d}{||M \d||}\]

transforming points, directions, normals

However, transforming a normal \(\n\) (perpendicular unit vector) by the transformation matrix \(M\) is done by multiplying with the inverse transpose of \(M\) followed by a normalization.

\[\frac{(M^T)^{-1} \n}{||(M^T)^{-1} \n||}\]

Proof:

• By definition: \(\t \cdot \n = \t^T\n = 0\)
• After transform: \((M \t)^T (X \n) = 0\)
• For all \(\t\) we have: \(\t^T M^T X \n = 0\)
• Which gives: \(\t^T M^T (M^T)^{-1} \n = 0\)
• Note: \((M^T)^{-1} = (M^{-1})^T\)

what if normal isn't given?

Surface normal can be computed as normalized cross product of two independent surface tangents

For triangle, choose two edges as tangents.

Gourard shading

Recall that Gourard shading is done by computing the "color" at each vertex of a triangle and interpolating these colors across the surface (varying vec3 v_color).

Phong shading

Phong shading interpolates the normal of each vertex across the triangle and computes the "color" at each fragment (varying vec3 v_normal).