Projection

COS 350 - Computer Graphics

perspective projection in drawing

perspective projection in drawing

perspective was not used until circa 15th century

technical explanation by Leon Battista Alberti

1436, De Pictura – Della Pittura

“

Trovai adunque io questo modo ottimo cosi in tutte le cose seguendo quanto dissi, ponendo il punto centrico, traendo indi linee alle divisioni della giacente linea del quadrangolo.

”

perspective projection in drawing

perspective was not used until circa 15th century

technical explanation by Leon Battista Alberti

1436, De Pictura – Della Pittura

“

Trovai adunque io questo modo ottimo cosi in tutte le cose seguendo quanto dissi, ponendo il punto centrico, traendo indi linee alle divisioni della giacente linea del quadrangolo.

Therefore, I found this so great as in all things according to what I said , putting the centric point , then drawing lines to the divisions of the line lying quadrangle.

”

perspective projection in drawing

perspective projection in drawing

perspective projection in photography

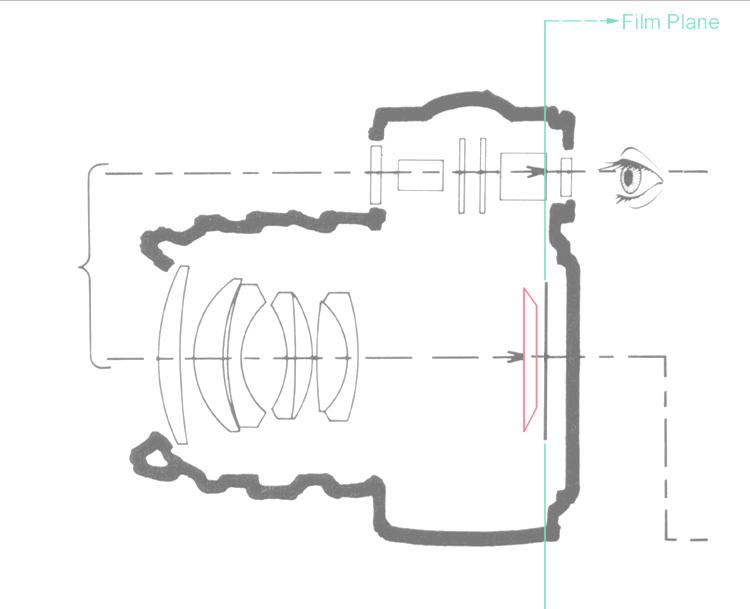
perspective projection in photography

raytracing vs. projection

ray tracing: image plane to object point

• start with image point
• generate a ray
• determine the visible object point

projection: object point to image plane

• start with an object point
• apply transforms
• determine the image plane point it projects to

inverse process

viewing

maps 3D world points to 2D image plane positions

two stages:

• viewing transform
  • map world coordinates to camera coordinates
  • change of coordinate system
• projection
  • map camera coordinates to image plane coordinates
  • orthographic or perspective

viewing transform

any affine transform

useful to define one for our viewer model

• defined by origin, forward, up

computed by

• orthonormalized frame from the vectors
• construct a matrix for a change of coord. system
• seen in previous lecture

projection

in general, function that transforms points from \(m\)-space to \(n\)-space, where \(m > n\)

in graphics, maps 3D points to 2D image coordinates

• except we will keep around the third coordinate

canonical view volume

the result of a projection

• everything projected out of it will not be rendered

\((x,y)\) are image plane coordinates in \([-1,1] \times [-1,1]\)

keep around the \(z\) normalized in \([-1,1]\)

• define a near and far distance
• everything on the near plane has \(z=1\)
• everything on the far plane has \(z=-1\)
• inverted \(z\)!
  • will become useful later on

canonical view volume

why introduce near/far clipping planes?

• mostly to reduce \(z\) range, motivated later

taxonomy of projections

orthographic projection

box view volume

orthographic projection

viewing rays are parallel

orthographic projection

center around the \(\z\) axis

\[\mat{x' \\ y' \\ z'} = \mat{x/r \\ y/t \\ (2z - n - f)/(n-f)}\]

orthographic projection

in matrix form

\[O = \mat{1/r & 0 & 0 & 0 \\ 0 & 1/t & 0 & 0 \\ 0 & 0 & 2/(n-f) & -(n+f)/(n-f) \\ 0 & 0 & 0 & 1}\]

perspective projection

truncated pyramid view volume

perspective projection

viewing rays converge to a point

perspective projection

center around the \(\z\) axis

\[\mat{x' \\ y' \\ z'} = \mat{(nx)/(rz) \\ (ny)/(tz) \\ \cdots}\]

perspective projection

in matrix form

\[P = \mat{n/r & 0 & 0 & 0 \\ 0 & n/t & 0 & 0 \\ 0 & 0 & (f+n)/(n-f) & -2nf/(n-f) \\ 0 & 0 & 1 & 0}\]

projection matrices

• orthographic projection is affine
• perspective projection is not
  • does not map origin to origin
  • maps lines to lines
  • parallel lines do not remain parallel
  • length ratios are not preserved
  • closed under composition

projection matrices

• the given matrices are simplified cases
• should be able to define more general cases
  • non-centered windows
  • non-square windows
• can find derivation, but it is a simple extension of these
• note that systems have different conventions
  • pay attention to their definition
  • sometimes names are the same

general orthographic

\[O = \mat{ \frac{2}{r-l} & 0 & 0 & \frac{l+r}{l-r} \\ 0 & \frac{2}{t-b} & 0 & \frac{b+t}{b-t} \\ 0 & 0 & \frac{2}{n-f} & \frac{n+f}{n-f} \\ 0 & 0 & 0 & 1 }\]

general perspective

\[P = \mat{ \frac{2n}{r-l} & 0 & \frac{l+r}{l-r} & 0 \\ 0 & \frac{2n}{t-b} & \frac{b+t}{b-t} & 0 \\ 0 & 0 & \frac{f+n}{n-f} & \frac{-2nf}{n-f} \\ 0 & 0 & 1 & 0 }\]