Balanced Search Trees
COS 265 - Data Structures & Algorithms
symbol table review
| implementation | search\(^*\) | insert\(^*\) | delete\(^*\) | search\(^\dagger\) | insert\(^\dagger\) | delete\(^\dagger\) | ordered | ops on keys |
|---|---|---|---|---|---|---|---|---|
| seq search (unordered list) | \(N\) | \(N\) | \(N\) | \(N\) | \(N\) | \(N\) | equals() |
|
| binary search (ordered array) | \(\log N\) | \(N\) | \(N\) | \(\log N\) | \(N\) | \(N\) | X | compareTo() |
| BST | \(N\) | \(N\) | \(N\) | \(\log N\) | \(\log N\) | \(\sqrtN\) | X | compareTo() |
| goal | \(\log N\) | \(\log N\) | \(\log N\) | \(\log N\) | \(\log N\) | \(\log N\) | X | compareTo() |
\(^*\)guarantee, \(^\dagger\)average
Challenge: Guarantee performance
This lecture: 2-3 trees, left-leaning red-black BSTs, B-trees
balanced search trees
2-3 search trees
2-3 tree
Allow 1 or 2 keys per node
- 2-node: one key, two children
- 3-node: two keys, three children
Symmetric order: Inorder traversal yields keys in ascending order
Perfect balance: Every path from root to null link has same length (how to maintain?)

2-3 tree demo
Search
- Compare search key against keys in node
- Find interval containing search key
- Follow associated link (recursively)
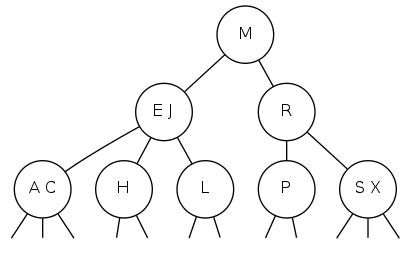
2-3 tree demo

2-3 tree demo

2-3 tree demo

2-3 tree demo

2-3 tree demo

2-3 tree demo

2-3 tree demo

2-3 tree demo

2-3 tree: insertion
Insertion into a 2-node at bottom
- Add new key to 2-node to create a 3-node

2-3 tree: insertion
Insertion into a 3-node at bottom
- Add new key to 3-node to create temporary 4-node
- Move middle key in 4-node into parent
- Repeat up the tree, as necessary
- If you reach the root and it's a 4-node, split it into three 2-nodes

2-3 tree: global properties
Invariants: Maintains symmetric order and perfect balance
Pf: Each transformation maintains symmetric order and perfect balance







2-3 tree: performance
Splitting a 4-node is a local transformation: constant number of operations


balanced search trees: quiz 1
What is the range of heights of a 2-3 tree with \(N\) keys (best / worst case)?
A. \(\texttilde \log_4 N\) / \(\texttilde \log_3 N\)
B. \(\texttilde \log_3 N\) / \(\texttilde \log_2 N\)
C. \(\texttilde \log_3 N\) / \(\texttilde 2 \log_2 N\)
D. \(\texttilde \log_3 N\) / \(\texttilde N\)
E. I don't know
2-3 tree: performance
Perfect balance: Every path from root to null link has same length

Tree height:
- Worst case: \(\lg N\) (all 2-nodes)
- Best case: \(\log_3 N \approx 0.631 \lg N\) (all 3-nodes)
- Between 12 and 20 for a million nodes
- Between 18 and 30 for a billion nodes
Bottom line: Guaranteed logarithmic performance for search and insert
ST implementation: summary
| implementation | search\(^*\) | insert\(^*\) | delete\(^*\) | search\(^\dagger\) | insert\(^\dagger\) | delete\(^\dagger\) | ordered | ops on keys |
|---|---|---|---|---|---|---|---|---|
| seq search (unordered list) | \(N\) | \(N\) | \(N\) | \(N\) | \(N\) | \(N\) | equals() |
|
| binary search (ordered array) | \(\log N\) | \(N\) | \(N\) | \(\log N\) | \(N\) | \(N\) | X | compareTo() |
| BST | \(N\) | \(N\) | \(N\) | \(\log N\) | \(\log N\) | \(\sqrtN\) | X | compareTo() |
| 2-3 tree\(^\ddagger\) | \(\log N\) | \(\log N\) | \(\log N\) | \(\log N\) | \(\log N\) | \(\log N\) | X | compareTo() |
\(^*\)guarantee, \(^\dagger\)average
\(^\ddagger\)but hidden constant \(c\) is large (depends upon implementation)
2-3 tree: implementation??
Direct implementation is complicated, because
- Maintaining multiple node types is cumbersome
- Need multiple compares to move down tree
- Need to move back up the tree to split 4-nodes
- Large number of cases for splitting
// fantasy code
public void put(Key key, Value val) {
Node x = root;
while(x.getTheCorrectChild(key) != null) {
x = x.getTheCorrectChildKey();
if(x.is4Node()) x.split();
}
if (x.is2Node()) x.make3Node(key, val);
else if(x.is3Node()) x.make4Node(key, val);
}
Bottom line: Could do it, but there's a better way
balanced search trees
red-black BSTs
how to implement 2-3 trees with binary trees?
Challenge: How to represent a 3-node?

how to implement 2-3 trees with binary trees?
Challenge: How to represent a 3-node?
Approach 1: Regular BST
- No way to tell a 3-node from a 2-node
- Cannot map from BST back to 2-3 tree


how to implement 2-3 trees with binary trees?
Challenge: How to represent a 3-node?
Approach 2: Regular BST with red "glue" nodes
- Wastes space, wasted link
- Code probably messy


how to implement 2-3 trees with binary trees?
Challenge: How to represent a 3-node?
Approach 3: Regular BST with red "glue" links
- Widely used in practice
- Arbitrary restriction: red links lean left


left-leaning red-black BSTs
- Represent 2-3 tree as a BST
- Use "internal" left-leaning links as "glue" for 3-nodes
- Larger key of 3-node is root of red edge


left-leaning red-black BSTs
A 2-3 tree and corresponding red-black BST

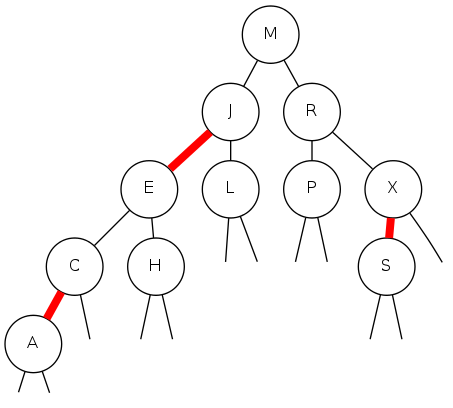
- Red links "glue" nodes within a 3-node
- Black links connect 2-nodes and 3-nodes
llrb BSTs: 1-1 correspondence with 2-3 trees
Key property: 1-1 correspondence between 2-3 and LLRB


an equivalent definition
A BST such that
- No node has two red links connected to it
- Every path from root to
nulllink has the same number of black links ("perfect black balance") - Red links lean left

search implementation for red-black BSTs
Observation: Search is the same as for elementary BST (ignore color), but runs faster because of better balance
public Value get(Key key) {
Node x = root;
while(x != null) {
int cmp = key.compareTo(x.key);
if (cmp < 0) x = x.left;
else if(cmp > 0) x = x.right;
else return x.val;
}
return null;
}
|
 |
Remark: Most other ops (e.g., floor, iteration, selection) are also identical
red-black bst representation
Each node is pointed to by precisely one link (from its parent); can encode color of links in nodes
private static final boolean RED = true;
private static final boolean BLACK = false;
private class Node {
Key key;
Value val;
Node left, right;
boolean color; // color of parent link
}
private boolean isRed(Node x) {
if(x == null) return false; // null links are black
return x.color == RED;
}
red-black bst representation

root.left.color == RED root.right.color == BLACK
insertion into a LLRB tree: overview
Basic strategy: Maintain 1-1 correspondence with 2-3 trees
During internal operations, maintain:
- Symmetric order
- Perfect black balance
- (but not necessarily color invariants)




How? Apply elementary red-black BST operations: rotation and color flip
elementary red-black BST operations
Left rotation: Orient a (temporarily) right-leaning red link to lean left
private node rotateLeft(Node h) {
assert isRed(h.right);
Node x = h.right;
h.right = x.left;
x.left = h;
x.color = h.color;
h.color = RED;
return x;
}
Invariants: Maintains symmetric order and perfect black balance
elementary red-black BST operations
Left rotation: Orient a (temporarily) right-leaning red link to lean left

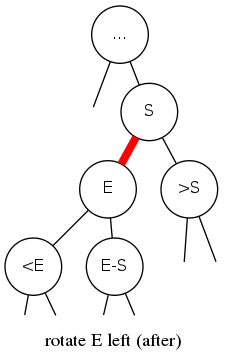
elementary red-black BST operations
Right rotation: Orient a left-leaning red link to (temporarily) lean right
private node rotateRight(Node h) {
assert isRed(h.left);
Node x = h.left;
h.left = x.right;
x.right = h;
x.color = h.color;
h.color = RED;
return x;
}
Invariants: Maintains symmetric order and perfect black balance
elementary red-black BST operations
Right rotation: Orient a left-leaning red link to (temporarily) lean right


elementary red-black BST operations
Color flip: Recolor to split a (temporary) 4-node
private void flipColors(Node h) {
assert !isRed(h);
assert isRed(h.left);
assert isRed(h.right);
h.color = RED;
h.left.color = BLACK;
h.right.color = BLACK;
}
Invariants: Maintains symmetric order and perfect black balance
elementary red-black BST operations
Color flip: Recolor to split a (temporary) 4-node


insertion into a LLRB tree
Warmup 1: Insert into a tree with exactly 1 node

- search ends at left
nulllink of root - red link to new node containing
Aconverts 2-node to 3-node
insertion into a LLRB tree
Warmup 1: Insert into a tree with exactly 1 node

- search ends at right
nulllink of root - red link to new node containing
B(right-leaning) - rotate left to make a legal (left-leaning) 3-node
insertion into a LLRB tree
Case 1: Insert into a 2-node at the bottom
- Do standard BST insert; color new link red (to maintain symmetric order and perfect black balance)
- If new red link is a right link, rotate left (to fix color invariants)

insertion into a LLRB tree
Case 1: Insert into a 2-node at the bottom
- Do standard BST insert; color new link red (to maintain symmetric order and perfect black balance)
- If new red link is a right link, rotate left (to fix color invariants)

insertion into a LLRB tree
Case 1: Insert into a 2-node at the bottom
- Do standard BST insert; color new link red (to maintain symmetric order and perfect black balance)
- If new red link is a right link, rotate left (to fix color invariants)

insertion into a LLRB tree
Warmup 2: Insert into a tree with exactly 2 nodes

- search ends at right
nulllink of root - attached new node with red link
- colors flipped to black
insertion into a LLRB tree
Warmup 2: Insert into a tree with exactly 2 nodes

- search ends at leftmost
nulllink - attached new node with red link
- rotated right
- colors flipped to black
insertion into a LLRB tree
Warmup 2: Insert into a tree with exactly 2 nodes

- search ends at left-right
nulllink - attached new node with red link
- rotated left, then rotated right
- colors flipped to black
insertion into a LLRB tree
Case 2: Insert into a 3-node at the bottom
- Do standard BST insert; color new link red to maintain symmetric order and perfect balance
- To fix color invariants:
- Rotate to balance the 4-node (if needed)
- Flip colors to pass red link up one level
- Rotate to make lean left (if needed)
- Repeat case 1 or case 2 up the tree (if needed)
insertion into a LLRB tree

- add new node (left of
R)
insertion into a LLRB tree

- add new node
- two lefts in a row, so rotate
Sright
insertion into a LLRB tree

- add new node
- two lefts in a row, so rotate right
- both children of
Rred, so flip colors
insertion into a LLRB tree

- add new node
- two lefts in a row, so rotate right
- both children of
Rred, so flip colors - right link of
Ered, so rotate left
insertion into a LLRB tree

- add new node
- two lefts in a row, so rotate right
- both children of
Rred, so flip colors - right link of
Ered, so rotate left
llrb bst construction demo

Insert E
llrb bst construction demo

Insert E
llrb bst construction demo

Insert A
llrb bst construction demo

Insert A
llrb bst construction demo
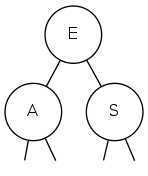
Insert R
llrb bst construction demo

Insert R
llrb bst construction demo

Insert C
llrb bst construction demo

Insert C
llrb bst construction demo

Insert H
llrb bst construction demo

Insert H
llrb bst construction demo

Insert X
llrb bst construction demo

Insert X
llrb bst construction demo

Insert M
llrb bst construction demo

Insert M
llrb bst construction demo

Insert P
llrb bst construction demo

Insert P
llrb bst construction demo
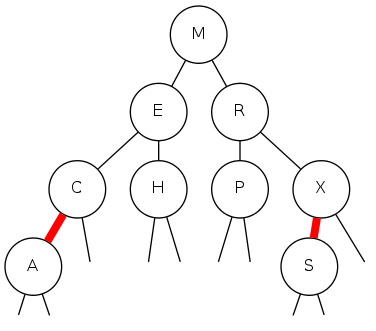
Insert L
llrb bst construction demo
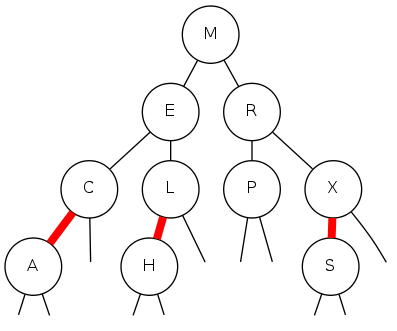
Insert L
insertion into LLRB: java implementation
Same code for all cases
- Right child red, left child black: rotate left
- Left child, left-left grandchild red: rotate right
- Both children red: flip colors
private Node put(Node h, Key key, Value val) {
if(h == null) {
// insert at bottom and color it red
return new Node(key, val, RED);
}
int cmp = key.compareTo(h.key);
if (cmp < 0) h.left = put(h.left, key, val);
else if(cmp > 0) h.right = put(h.right, key, val);
else h.val = val;
// only a few extra LoC provides near-perfect balance
// lean left
if(isRed(h.right) && !isRed(h.left)) h = rotateLeft(h);
// balance 4-node
if(isRed(h.left) && isRed(h.left.left)) h = rotateRight(h);
// split 4-node
if(isRed(h.left) && isred(h.right)) flipColors(h);
return h;
}
insertion into LLRB: visualization
255 insertions in ascending order

insertion into LLRB: visualization
255 insertions in descending order

insertion into LLRB: visualization
255 random insertions
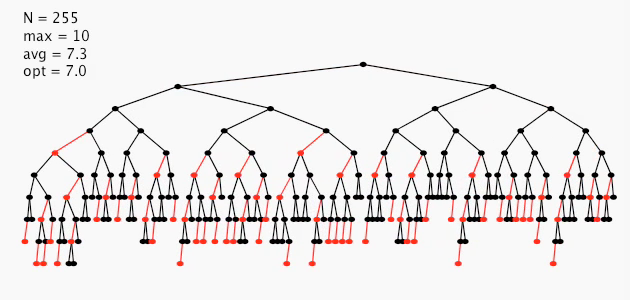
balanced search trees: quiz 2
What is the height of an LLRB tree with \(N\) keys in the worst case?
A. \(\texttilde \log_3 N\)
B. \(\texttilde \log_2 N\)
C. \(\texttilde 2 \log_2 N\)
D. \(\texttilde N\)
E. I don't know
balance in LLRB trees
Proposition: Height of tree is \(\leq 2 \log N\) in the worst case
Pf:
- Black height \(=\) height of corresponding 2-3 tree \(\leq \lg N\)
- Never two red links in a row

Property: Height of tree is \(\texttilde 1.0 \lg N\) in typical applications
ST implementation: summary
| implementation | search\(^*\) | insert\(^*\) | delete\(^*\) | search\(^\dagger\) | insert\(^\dagger\) | delete\(^\dagger\) | ordered | ops on keys |
|---|---|---|---|---|---|---|---|---|
| seq search (unordered list) | \(N\) | \(N\) | \(N\) | \(N\) | \(N\) | \(N\) | equals() |
|
| binary search (ordered array) | \(\log N\) | \(N\) | \(N\) | \(\log N\) | \(N\) | \(N\) | X | compareTo() |
| BST | \(N\) | \(N\) | \(N\) | \(\log N\) | \(\log N\) | \(\sqrtN\) | X | compareTo() |
| 2-3 tree\(^\ddagger\) | \(\log N\) | \(\log N\) | \(\log N\) | \(\log N\) | \(\log N\) | \(\log N\) | X | compareTo() |
| LLRB\(^\star\) | \(\log N\) | \(\log N\) | \(\log N\) | \(\log N\) | \(\log N\) | \(\log N\) | X | compareTo() |
\(^*\)guarantee, \(^\dagger\)average
\(^\ddagger\)hidden constant \(c\) is large (depends upon implementation)
\(^\star\)hidden constant \(c\) is small (at most \(2 \lg N\) compares)
war story: why red-black?
|
Xerox PARC innovations (1970s)
|
  |
war story: red-black BSTs
Telephone company contracted with database provider to build real-time database to store customer information
Database implementation
- Red-Black BST
- Exceeding height limit of 80 triggered error-recovery process (show allow for up to \(2^{40} > 10^{12}\) keys)
war story: red-black BSTs
Telephone company contracted with database provider to build real-time database to store customer information
Extended telephone service outage
- Main cause: height bound exceeded (did not rebalance BST during delete)
- Telephone company sues database provider
- Legal testimony:
“If implemented properly, the height of a red-black BST with \(N\) keys is at most \(2 \lg N\).
”
—expert witness
balanced search trees
B-trees
file system model
- Page
- contiguous block of data (e.g., a 4096-byte chunk)
- Probe
- first access to a page (e.g., from disk to memory)


Property: time required for a probe is much larger than time to access data within a page
Cost model: number of probes
Goal: access data using minimum number of probes
b-trees (bayer-mccreight, 1972)
B-tree: Generalize 2-3 trees by allowing up to \(M\) keys per node
- Choose \(M\) as large as possible so that \(M\) keys fit in a page (\(M = 1024\) is typical)
- At least \(\left\lfloor M/2 \right\rfloor\) keys in all nodes (except root)
- Every path from root to leaf has same number of links

search in a b-tree
- Start at root
- Check if node contains key
- Otherwise, find interval for search key and take corresponding link
- Could use binary search, but all ops are considered free

Insertion in a B-tree
- Search for new key
- Insert at bottom
- Split nodes with \(M+1\) keys on the way back up the B-tree, moving middle key to parent

balance in b-tree
Proposition: A search or an insertion in a B-tree of order \(M\) with \(N\) keys requires between \(\texttilde \log_M N\) and \(\texttilde \log_{M/2} N\) probes.
Pf: All nodes (except possibly root) have between \(\left\lfloor M/2 \right\rfloor\) and \(M\) keys
In practice: Number of probes is at most \(4\) (when \(M=1024\), \(N = 62 \text{ billion}\), then \(\log_{M/2} N \leq 4\))
balanced search trees: quiz 3
What of the following does the B in B-tree not mean?
A. Bayer
B. Balanced
C. Binary
D. Boeing
E. I don't know
“the more you think about what the B in B-trees could mean, the more you learn about B-trees and that is good.
”
–Ed McCreight
balanced trees in the wild
Red-Black trees are widely used as system symbol tables
- Java:
java.util.TreeMap,java.util.TreeSet - C++ STL: map, multimap, multiset
- Linux kernel: completely fair scheduler,
linux/rbtree.h - Emacs: conservative stack scanning
B-tree cousins: B+ tree, B*tree, B# tree, ...
B-trees (and cousins) are widely used for file systems and DBs
- Windows: NTFS
- Mac: HFS, HFS+
- Linux: ReiserFS, XFS, Ext3FS, JFS, BTRFS
- Databases: ORACLE, DB2, INGRES, SQL, PostgreSQL
