Geometric Applications of BSTs
COS 265 - Data Structures & Algorithms
overview
This lecture: intersections among geometric objects


Applications: CAD, games, movies, virtual reality, databases, GIS, ...
Efficient solutions: Binary search trees (and extensions)
overview
This lecture is only the tip of the iceberg!
See COS 350 and COS 424!
Geometric Applications of BSTs
1D range search
1d range search
Extension of ordered symbol table
- Insert key-value pair
- Search for key
k - Delete key
k - Range search: find all keys between
k1andk2 - Range count: find number of keys between
k1andk2
Application: database queries
1d range search
insert B B insert D B D insert A A B D insert I A B D I insert H A B D H I insert F A B D F H I insert P A B D F H I P search G to K H I count G to K 2
Geometric interpretation
- Keys are points on a line
- Find/count points in a given 1d interval

Quiz 1
Suppose that the keys are stored in a sorted array. What is the order of growth of the running time to perform range count as a function of \(N\) and \(R\), where \(N\) is number of keys and \(R\) is number of matching keys?
A. \(\log R\)
B. \(\log N\)
C. \(\log N + R\)
D. \(N + R\)
E. I don't know
1d range search: elementary impl
Ordered array: slow insert; fast range search
Unordered list: slow insert; slow range search
| data structure | insert | range count | range search |
|---|---|---|---|
| ordered array | \(N\) | \(\log N\) | \(R + \log N\) |
| unordered list | \(N\) | \(N\) | \(N\) |
| goal | \(\log N\) | \(\log N\) | \(R + \log N\) |
\(N\) is number of keys; \(R\) is number of keys that match
1d range count: BST implementation
1D range count: how many keys between lo and hi, inclusively?
public int size(Key lo, Key hi) {
int rhi = rank(hi);
int rlo = rank(lo);
if(contains(hi))
return rhi-rlo+1;
else
return rhi-rlo;
// num of keys < hi
}
|
 |
Proposition: running time proportional to \(\log N\), assuming BST is balanced.
Pf: Nodes examined = search path to lo + search path to hi
1d range search: BST implementation
1D range search: find all keys between lo and hi
- Recursively find all keys in left subtree if any could fall in range
- Check key in current node
- Recursively find all keys in right subtree if any could fall in range
1d range search: BST implementation

keys(E,Q) => {E, G, H, L, M, P}
1d range search: BST implementation
Proposition: running time proportional to \(R + \log N\)
Proof: Nodes examined = search path to lo + search path to hi + matches
1d range search: summary of performance
Ordered array: slow insert; fast range search
Unordered list: slow insert, slow range search
BST: fast insert, fast range search
| data structure | insert | range count | range search |
|---|---|---|---|
| ordered array | \(N\) | \(\log N\) | \(R + \log N\) |
| unordered list | \(N\) | \(N\) | \(N\) |
| goal | \(\log N\) | \(\log N\) | \(R + \log N\) |
\(N\) is number of keys; \(R\) is number of keys that match
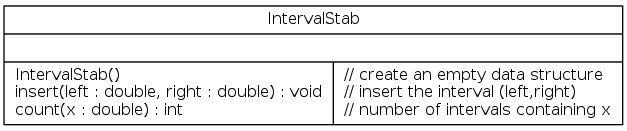
Exercise: interval stabbing query
Goal: Insert intervals (left,right) and support queries of the form "how many intervals contain x?"

Geometric applications of bsts
line segment intersection
orthogonal line segment intersection
Given \(N\) horizontal and vertical line segments, find all intersections

Quadratic algorithm: Check all pairs of line segments for intersections
microprocessors and geometry
Early 1970s: microprocessor design became a geometric problem
- Very Large Scale Integration (VLSI)
- Computer-Aided Design (CAD)
Design-rule checking
- Certain wires cannot intersect
- Certain spacing needed between different types of wires
- Debugging = line segment (or rectangle) intersection


algorithms and moore's law
Moore's law (1965): Transistor count doubles every 2 years
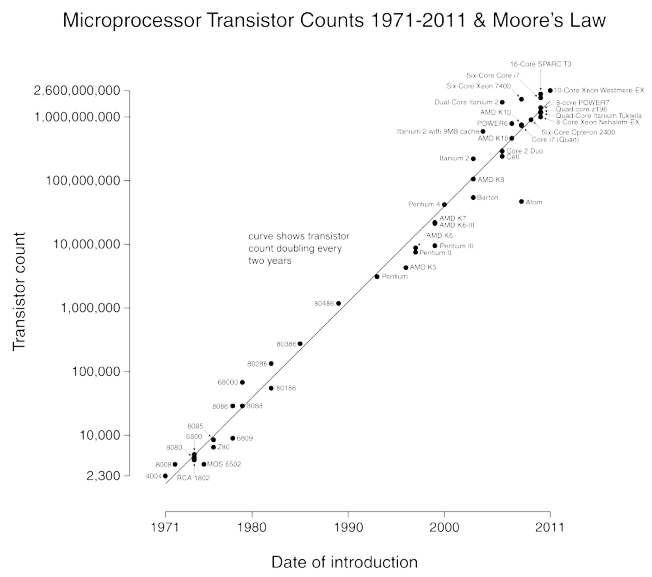

Sustaining Moore's law
Sustaining Moore's law
- problem size doubles every 2 years (problem size = transistor count)
- processing power doubles every 2 years (get to use faster computer)
- How much $ do I need to get the job done with a quadratic algorithm?
Running time today: \(T_N = a N^2\)
Running time in 2 years: \(T_{2N} = (a/2)(2N)^2 = 2T_N\)
Sustaining Moore's law
| running time | 1970 | 1972 | 1974 | 2000 |
|---|---|---|---|---|
| \(N\) | $ \(x\) | $ \(x\) | $ \(x\) | $ \(x\) |
| \(N \log N\) | $ \(x\) | = $ \(x\) | = $ \(x\) | = $ \(x\) |
| \(N^2\) | $ \(x\) | $ \(2x\) | $ \(4x\) | $ \(2^nx\) |
where \(n = 15\)
Bottom line: Linearithmic algorithm is necessary to sustain Moore's law
orthogonal line segment intersection: sweep-line algorithm
Nondegeneracy assumption: All x- and y- coordinates are distinct

orthogonal line segment intersection: sweep-line algorithm
Sweep vertical line from left to right
- x-coordinates define events
- h-segment (left endpoint): insert y-coordinate into BST
- h-segment (right endpoint): remove y-coordinate from BST
- v-segment: range search for interval of y-endpoints

orthogonal line segment intersection: sweep-line algorithm
Sweep vertical line from left to right
- x-coordinates define events
- h-segment (left endpoint): insert y-coordinate into BST
- h-segment (right endpoint): remove y-coordinate from BST
- v-segment: range search for interval of y-endpoints

orthogonal line segment intersection: sweep-line algorithm
Sweep vertical line from left to right
- x-coordinates define events
- h-segment (left endpoint): insert y-coordinate into BST
- h-segment (right endpoint): remove y-coordinate from BST
- v-segment: range search for interval of y-endpoints
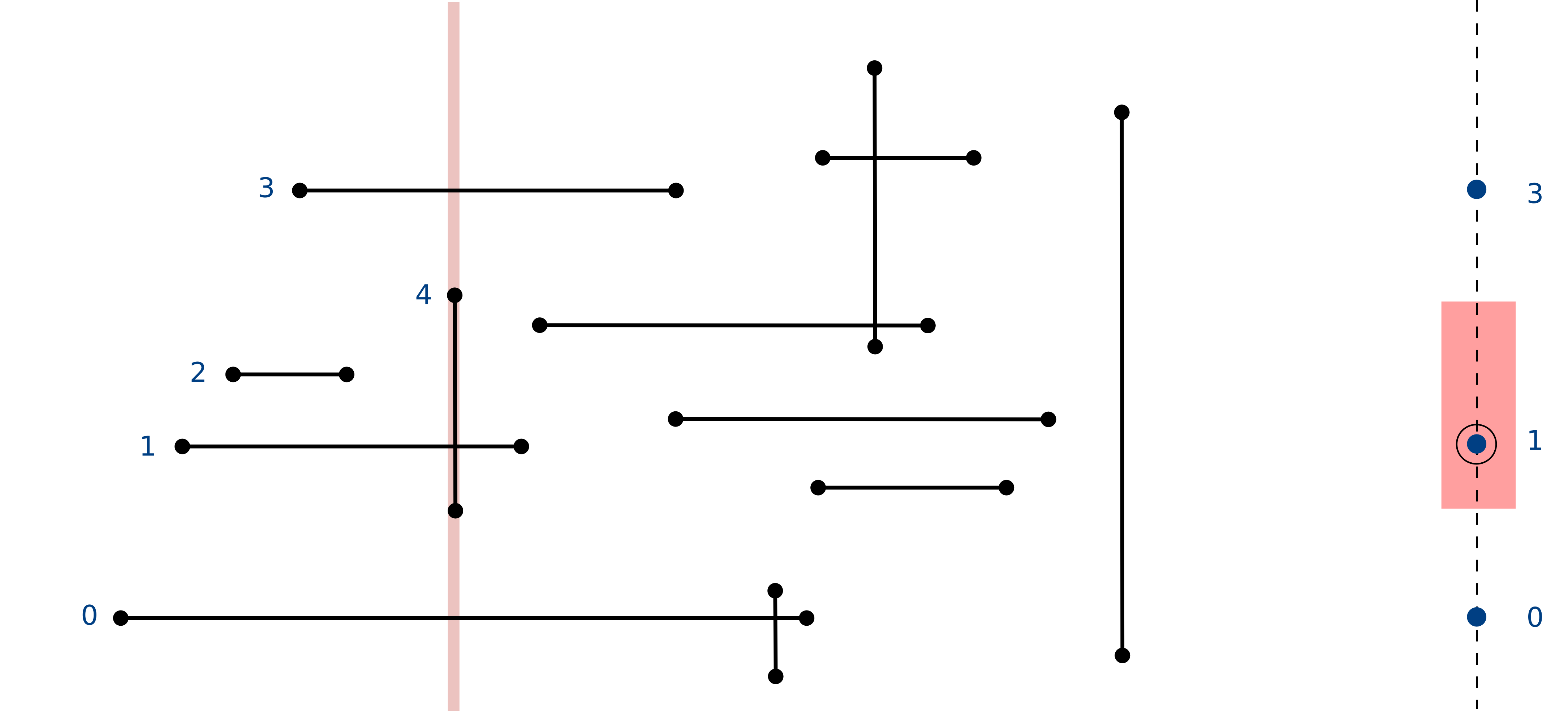
orthogonal line segment intersection: sweep-line algorithm
Proposition: the sweep-line algorithm takes time proportional to \(N \log N + R\) to find all \(R\) intersections among \(N\) orthogonal line segments
Proof:
- Put x-coordinate on a PQ (or sort) (\(N \log N\))
- Insert y-coordinate into BST (\(N \log N\))
- Delete y-coordinate from BST (\(N \log N\))
- Range searches is BST \(N \log N + R\)
Bottom line: sweep line reduces 2D orthogonal line segment intersection search to 1D range search
sweep-line algorithm: context
The sweep-line algorithm is a key technique in computation geometry
Geometric intersection
- General line segment intersection
- Axis-aligned rectangle intersection
- ...


sweep-line algorithm: context
More problems
- Andrew's algorithm for convex hull
- Fortune's algorithm Voronoi diagram
- Scanline algorithm for rendering computer graphics
- Generating slices for additive 3D printing
- ...

geometric applications of bsts
\(k\)-d trees
2D orthogonal range search
Extension of ordered symbol-table to 2D keys
- Insert a 2D key
- Search for a 2D key
- Delete a 2D key
- Range search: find all keys that lie in a 2D range
- Range count: number of keys that lie in a 2D range
Applications: Networking, circuit design, databases, ...
2D orthogonal range search
Geometric interpretation
- Keys are points in the plane
- Find/count points in a given h-v rectangle (axis-aligned)

2D ortho search: grid implementation
|
Grid implementation
|
 |
2D ortho search: grid impl. analysis
Space-time tradeoff
- Space: \(M^2 + N\)
- Time: \(1 + N / M^2\) per square examined, on average
Choose grid square size to tune performance
- Too small: wastes space
- Too large: too many points per square
- General rule: \(\sqrt{N}\)-by-\(\sqrt{N}\) grid
2D ortho search: grid impl. analysis
Running time (if points are evenly distributed)
- Choose \(M \texttilde \sqrt{N}\)
- Initialize data structure: \(N\)
- Insert point: \(1\)
- Range search: \(1\) per point in range
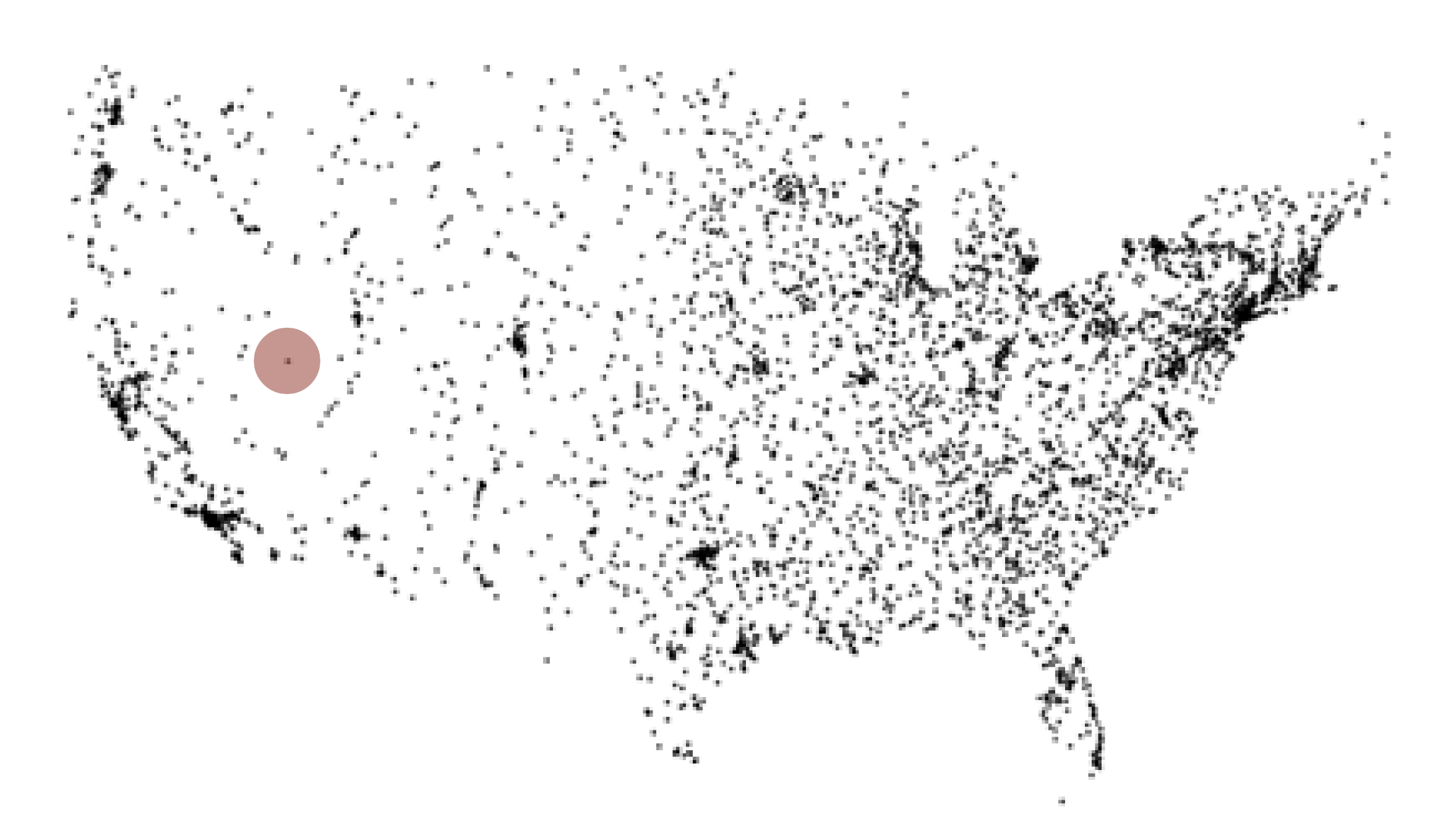
clustering
grid implementation: fast, simple solution for evenly-distributed points
Problem: Clustering is a well-known phenomenon in geometric data
- Lists are too long, even though average length is short
- Need data structure that adapts gracefully to data

clustering
grid implementation: fast, simple solution for evenly-distributed points
Problem: Clustering is a well-known phenomenon in geometric data
Example: USA Map data


13,000 points, 1000 grid squares: half the squares are empty, and half the points are in 10% of the squares
space-partitioning trees
Use a tree to represent a recursive subdivision of 2D space
- Grid: divide space uniformly into squares
- Quadtree: recursively divide space into four quadrants
- 2D tree: recursively divide space into two axis-aligned halfplanes
- BSP tree: recursively divide space into two arbitrary halfplanes




space-partitioning trees: applications
|
Applications
|

|
2d tree construction
Recursively partition plane into two halfplanes


2d tree implementation
Data structure: BST, but alternate using \(x\)- and \(y\)-coordinate as key
- Search gives rectangle containing point
- Insert further subdivides the plane




quiz 2
Where would point 11 be inserted in the \(k\)-d tree below?
|
A. Right child of F |


quiz 2
Where would point 11 be inserted in the \(k\)-d tree below?
|
A. Right child of F |
F is LR node, so right = right |


2d tree demo: range search
Goal: Find all points in a query axis-aligned rectangle
- Check if point in node lies in given rectangle
- Recursively search left/bottom if any could fall in rectangle
- Recursively search right-top if any could fall in rectangle

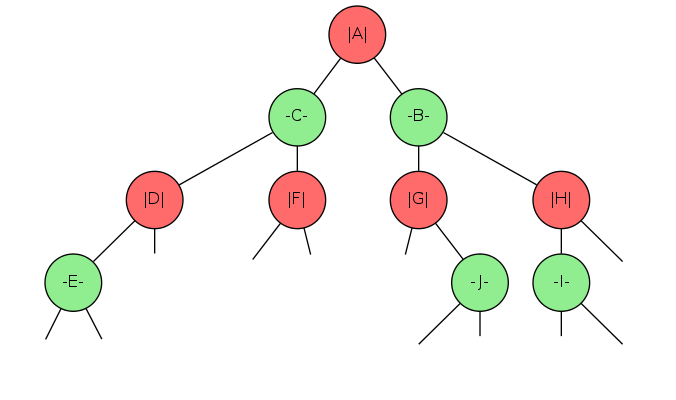
range search in a 2d tree analysis
Typical case: \(R + \log N\)
Worst case (assuming tree is balanced): \(R + \sqrt{n}\)


2d tree demo: nearest neighbor
Goal: Find closest point to query point
- Check distance from point in node to query point
- Recursively search left/bottom if it could contain a closer point
- Recursively search right/top if it could contain a closer point
- Organize method so that it begins by searching for query point

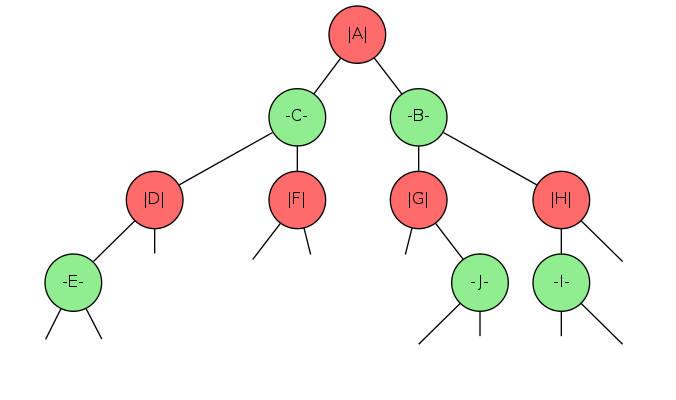
Quiz 3
Which of the following is the worst case for nearest neighbor search?
|
A. B. |
C. D. I don't know |
nn search in a 2d tree analysis
Typical case: \(\log N\)
Worst case (even if tree is balanced): \(N\)


\(k\)-d tree
\(k\)-d tree: Recursively partition \(k\)-dimensional space into 2 halfspaces
Implementation: BST, but cycle through dimensions as in 2D trees


\(k\)-d tree
Efficient, simple data structure for processing \(k\)-dimensional data
- Widely used
- Adapts well to high-dimensional and clustered data
- Discovered by an undergrad in an algorithms class

flocking birds
Q. What "natural algorithm" do starlings, migrating geese, cranes, bait balls of fish, and flashing fireflies use to flock?
flocking boids (craig reynolds, 1986)
Boids: 3 simple rules lead to complex emergent flocking behavior:
- Collision avoidance: point away from \(k\)-nearest boids
- Flock centering: point towards center mass of \(k\)-nearest boids
- Velocity matching: update velocity to avg of \(k\)-nearest boids
\(N\)-body simulation
Goal: simulate motion of \(N\) particles, mutually affected by gravity
Brute force: for each pair of particles, compute force: \(F = \frac{Gm_1m_2}{r^2}\)
Running time: time per step is \(N^2\)
appel's algorithm for \(N\)-body simulation
Key idea: Suppose particle is far, far away from cluster of particles
- Treat cluster of particles as a single aggregate particle
- Compute force between particle and center of mass of aggregate

appel's algorithm for \(N\)-body simulation
- Build 3D tree with \(N\) particles as nodes
- Store center-of-mass of subtree in each node
- To compute total force acting on a particle, traverse tree, but stop as soon as distance from particle to subdivision is sufficiently large

Impact: running time per step is \(N \log N\), enabling new research!
geometric applications of BSTs
| problem | example | solution |
|---|---|---|
| 1d range search |  |
binary search tree |
| 2d ortho line segment intersection |  |
sweep line reduces problem to 1d range search |
| 2d range search, kd range search |  |
2d tree, kd tree |
orthogonal rectangle intersection
Goal: Find all intersections among a set of \(N\) orthogonal rectangles
Quadratic algorithm: Check all pairs of rectangles for intersections

Non-degeneracy assumption: all \(x\)- and \(y\)-coordinates are distinct
ortho rect intersection: sweep-line algo
Sweep vertical line from left to right
- \(x\)-coordinates of left and right endpoints define events
- Maintain set of rectangles that intersect the sweep line in an interval search tree (using \(y\)-intervals of rectangle)
- Left endpoint: interval search for \(y\)-interval of rectangle; insert \(y\)-interval
- Right endpoint: remove \(y\)-interval

ortho rect intersection: sweep-line analysis
Proposition: sweep line algorithm takes time proportional to \(N \log N + R \log N\) to find \(R\) intersections among a set of \(N\) rectangles
Pf:
- Put \(x\)-coordinates on a PQ or sort (\(N \log N\))
- Insert \(y\)-intervals into ST (\(N \log N\))
- Delete \(y\)-intervals from ST (\(N \log N\))
- Interval searches for \(y\)-intervals (\(N \log N + R \log N\))
Bottom line: Sweep line reduces 2D orthogonal rectangle intersection search to 1D interval search
geometric applications of BSTs
| problem | example | solution |
|---|---|---|
| 1d range search |  |
binary search tree |
| 2d ortho line segment intersection |  |
sweep line reduces problem to 1d range search |
| 2d range search, kd range search |  |
2d tree, kd tree |
| 2d ortho rectangle intersection |  |
sweep line reduces problem to 1d interval search |