Binary Search Trees
COS 265 - Data Structures & Algorithms
Binary Search Trees
BSTs
Binary Search Trees
Definition: A BST is a binary tree in symmetric order
A binary tree is either
- empty
- two disjoint binary trees (left and right)
Symmetric order: Each node has a key and every node's key is
- larger than all keys in its left subtree
- smaller than all keys in its right subtree
Binary Search Trees
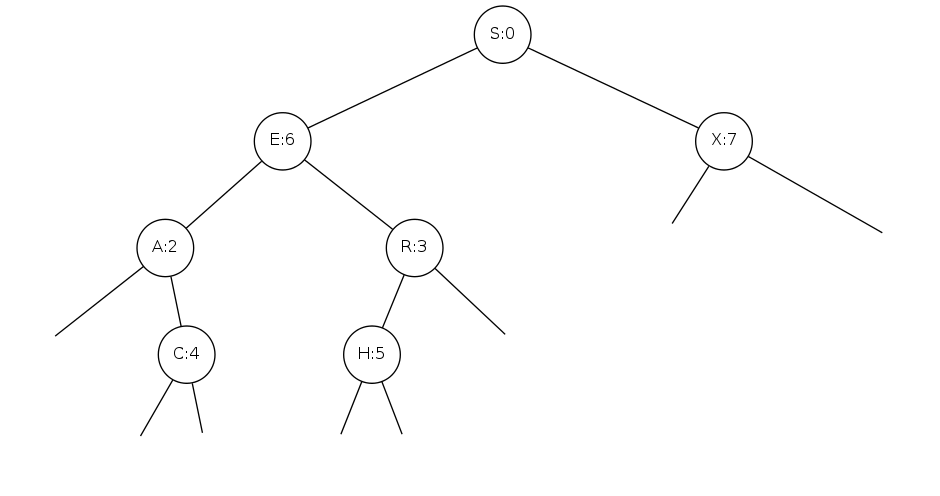
S-node is root of tree E-node is parent of A-node (left) and R-node (right) E-node and all children nodes is a subtree E-node has key = E, value = 6 All nodes in subtree rooted at A have keys smaller than E All nodes in subtree rooted at R have keys larger than E
binary search tree demo
Search: if less, go left; if greater, go right; if equal, search hit
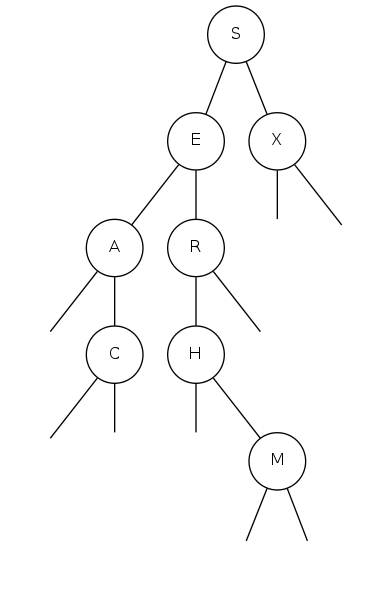
binary search tree demo
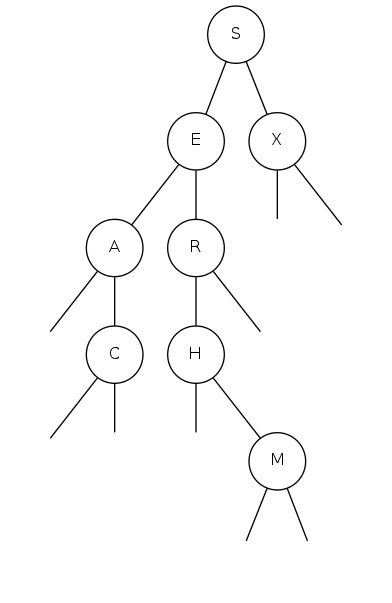
Search for A
binary search tree demo
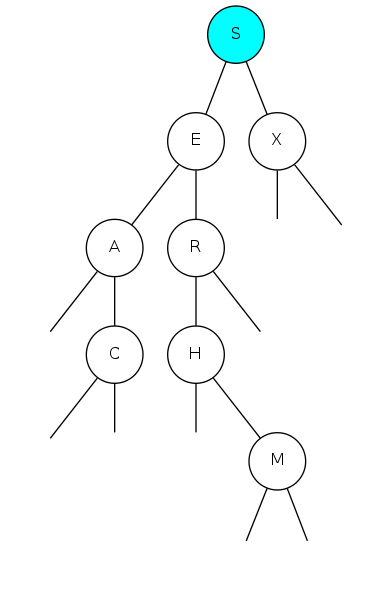
Search for A
binary search tree demo
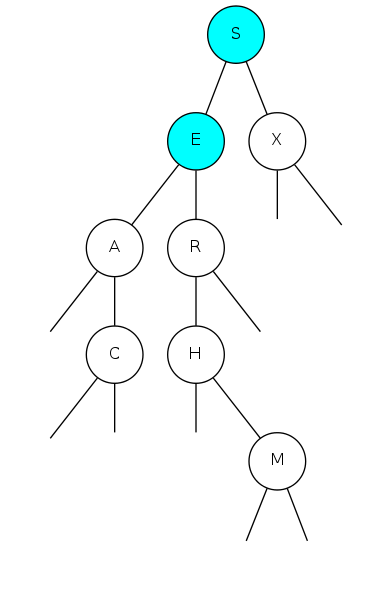
Search for A
binary search tree demo
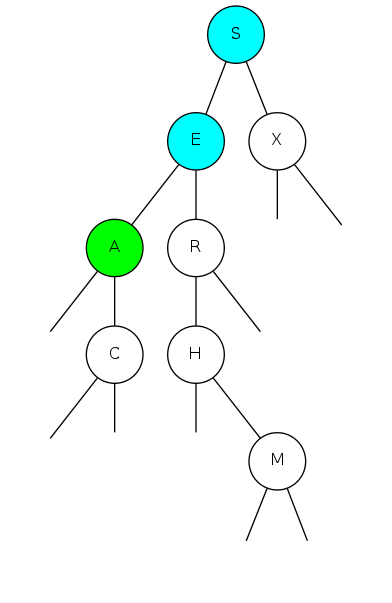
Search for A: Found!
binary search tree demo
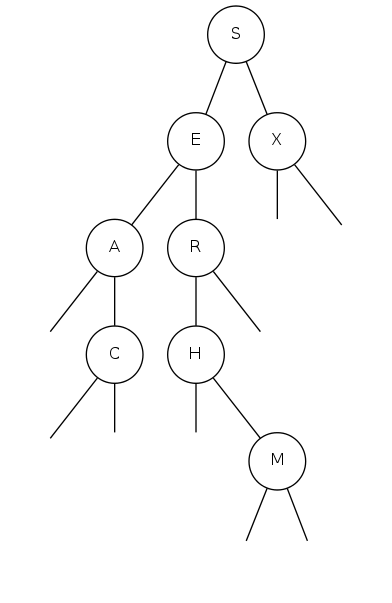
Search for F
binary search tree demo
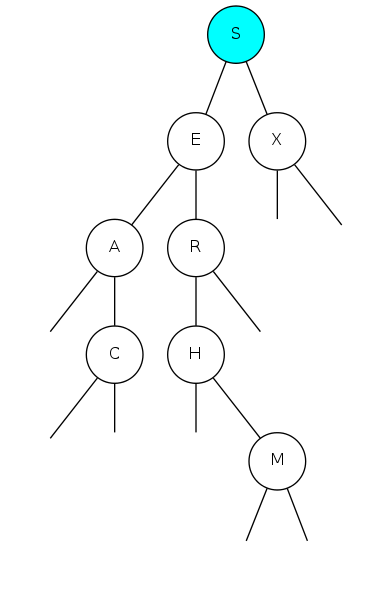
Search for F
binary search tree demo
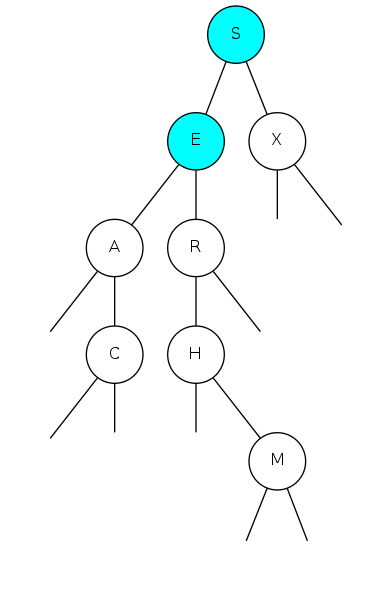
Search for F
binary search tree demo
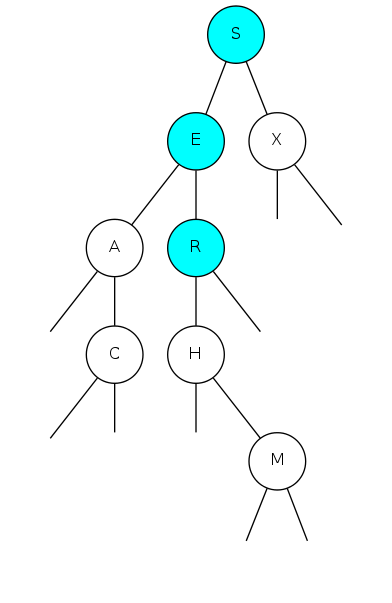
Search for F
binary search tree demo
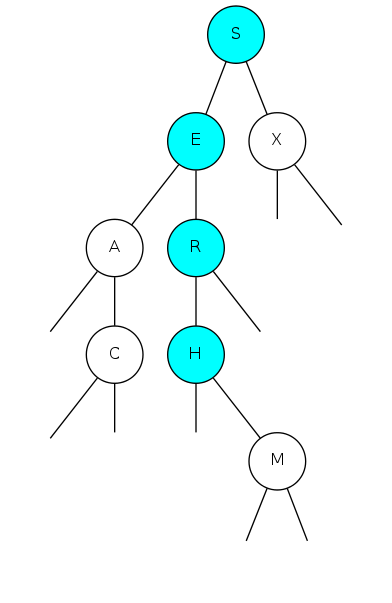
Search for F
binary search tree demo
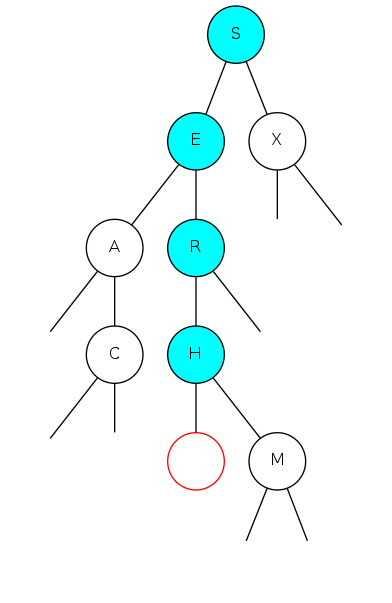
Search for F: Not found!
binary search tree demo
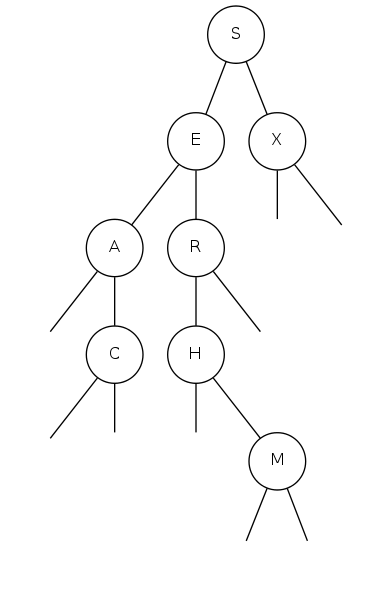
Insert U
binary search tree demo
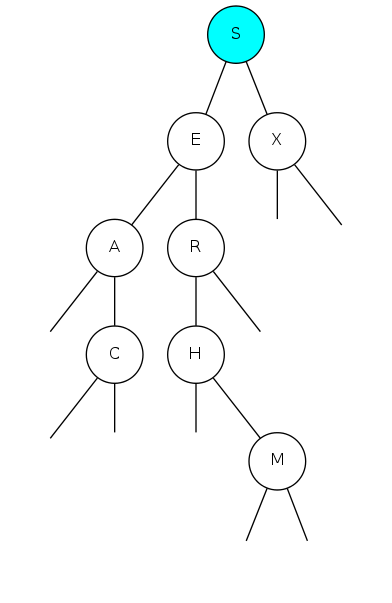
Insert U
binary search tree demo
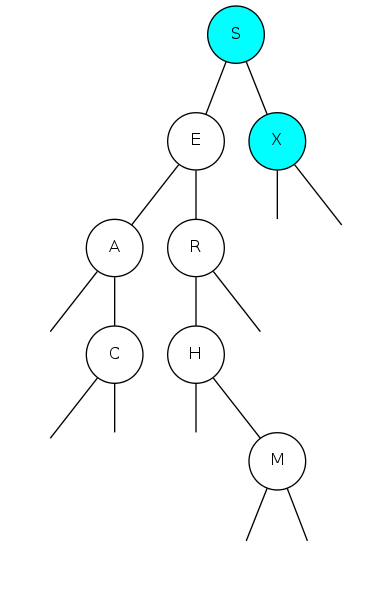
Insert U
binary search tree demo
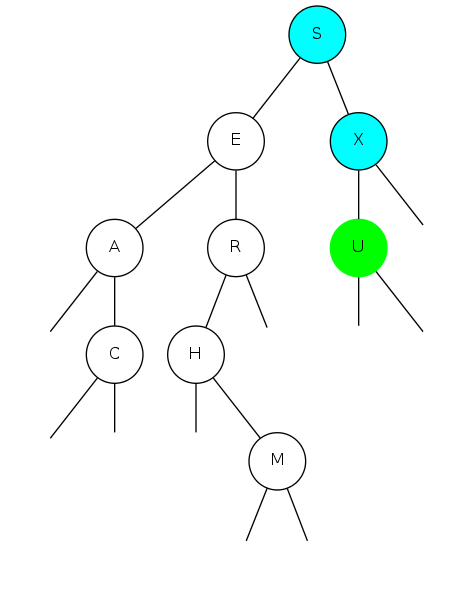
Insert U
bst representation in java
Java definition: A BST is a reference to a root Node
A Node is composed of four fields:
- A
Keyand aValue - A reference to the
leftandrightsubtree for smaller and larger keys (resp.)
// Key and Value are generic types; Key is Comparable
private class Node {
private Key key;
private Value val;
private Node left, right;
public Node(Key key, Value val) {
this.key = key;
this.val = val;
}
}
BST implementation (skeleton)
public class BST<Key extends Comparable<Key>, Value> {
private Node root; // root of BST
private class Node { /* prev slide */ }
public void put(Key key, Value val) { /* next slides */ }
public Value get(Key key) { /* next slides */ }
public void delete(Key key) { /* next slides */ }
public Iterable<Key> iterator() { /* next slides */ }
}
bst search: java implementation
Get: return value corresponding to given key, or null if no such key
public Value get(Key key) {
Node x = root;
while(x != null) {
int cmp = key.compareTo(x.key);
if (cmp < 0) x = x.left;
else if(cmp > 0) x = x.right;
else return x.val;
}
return null;
}
Cost: number of compares \(= 1 + \text{depth of node}\)
bst insert
|
Put: Associate value with key Search for key, then two cases:
|
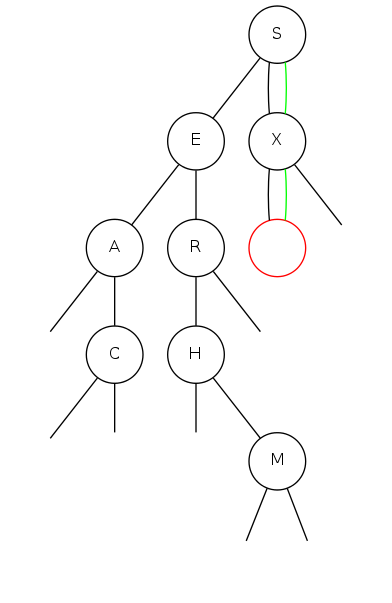 Insert |
bst insert
|
Put: Associate value with key Search for key, then two cases:
|
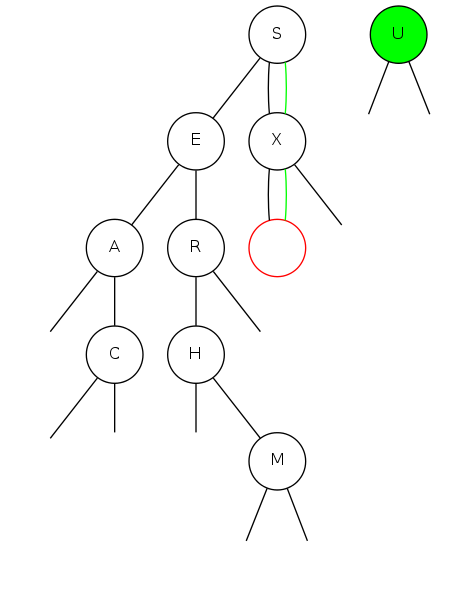 Insert |
bst insert
|
Put: Associate value with key Search for key, then two cases:
|
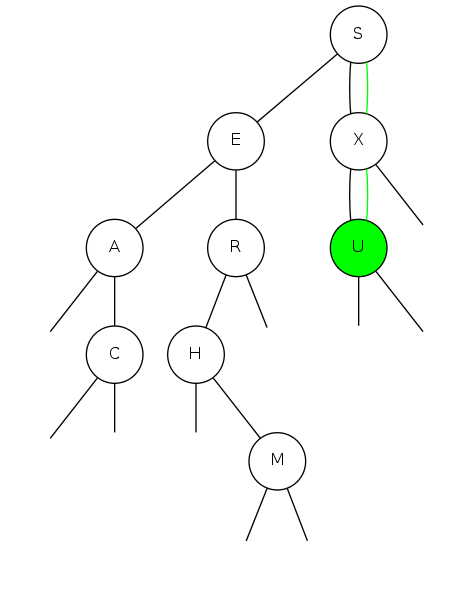 Insert |
bst insert: java implementation
Put: Associate value with key
public void put(Key key, Value val) {
root = put(root, key, val);
}
private Node put(Node x, Key key, Value val) {
if(x == null) return new Node(key, val);
int cmp = key.compareTo(x.key);
// concise, but tricky, recursive code; read carefully!!
if (cmp < 0) x.left = put(x.left, key, val);
else if(cmp > 0) x.right = put(x.right, key, val);
else x.val = val;
return x;
}
Cost: Number of compares \(= 1 + \text{depth of node}\)
tree shape
- Many BSTs correspond to same set of keys
- Number of compares for search/insert \(= 1 + \text{depth of node}\)
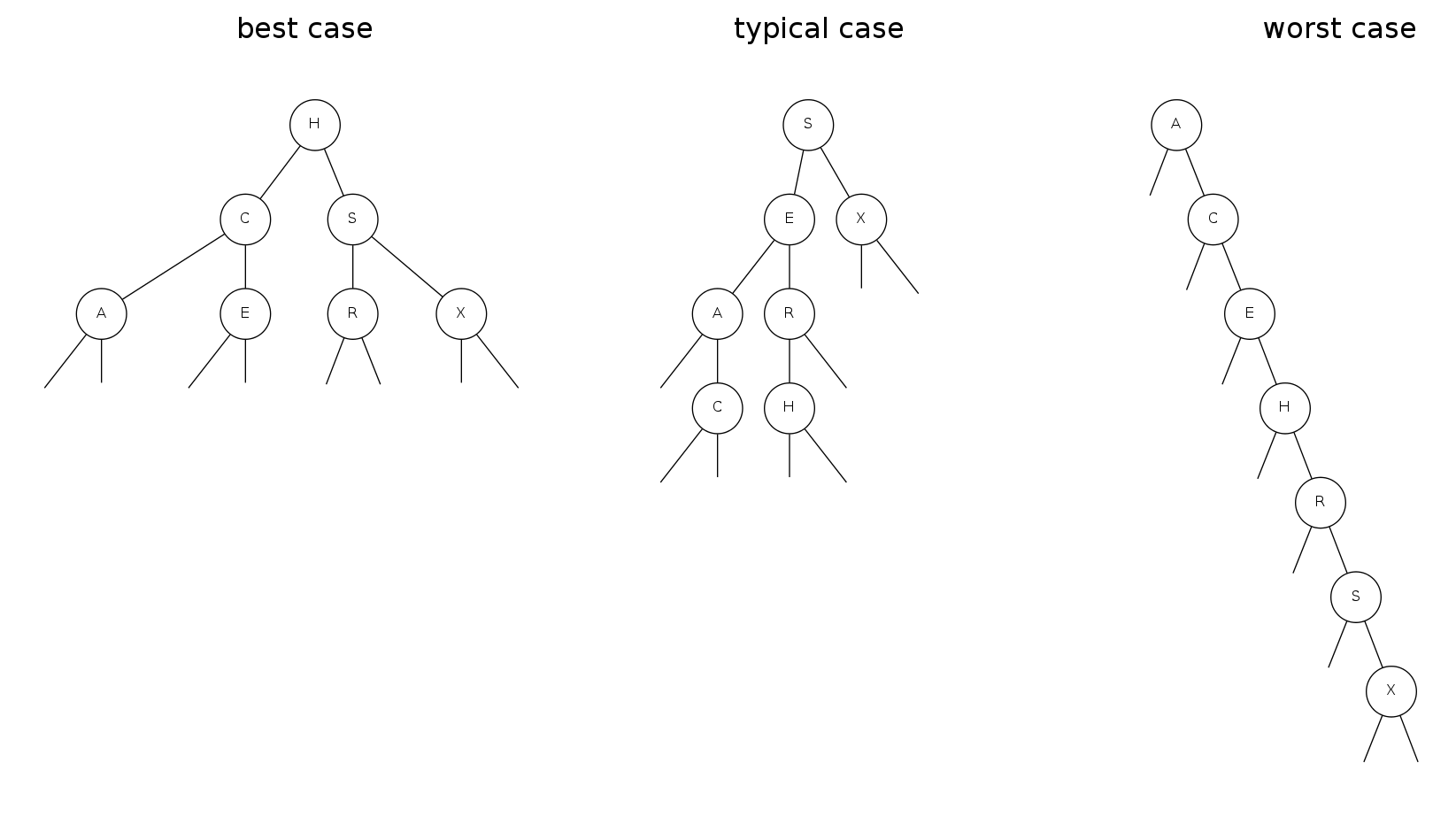
Bottom line: tree shape depends on order of insertion
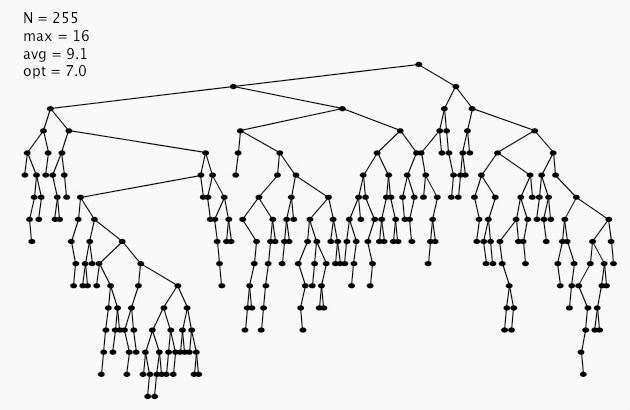
BST insertion: random order visualization
Ex: insert keys in random order
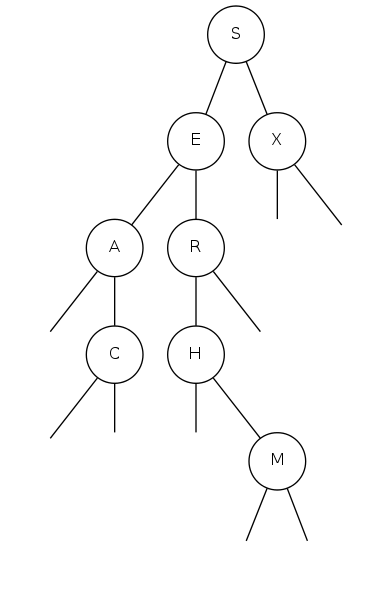
binary search trees: quiz 1
In what order does the traverse(root) code print out the keys in the BST?
private void traverse(Node x)
{
if(x == null) return;
traverse(x.left);
StdOut.println(x.key);
traverse(x.right);
}
A. A C E H M R S X |
 |
inorder traversal
- Traverse left subtree
- Enqueue key
- Traverse right subtree
// all keys, in order:
// [smaller keys, in order] key [larger keys, in order]
public Iterable<Key> keys() {
Queue<Key> q = new Queue<Key>();
inorder(root, q);
return q;
}
private void inorder(Node x, Queue<Key> q) {
if(x == null) return;
inorder(x.left, q);
q.enqueue(x.key);
inorder(x.right, q);
}
Property: Inorder traversal of a BST yields keys in ascending order
Binary search trees: quiz 2
What is the name of this sorting algorithm?
Shuffle the keys Insert the keys into a BST, one at a time Do an inorder traversal of the BST
A. Insertion sort
B. Mergesort
C. Quicksort
D. None of the above
E. I don't know
correspondence: BSTs and QS partitioning
0 1 2 3 4 5 6 7 8 9 0 1 2 3 P S E U D O M Y T H I C A L P S E U D O M Y T H I C A L | H L E A D O M C I|P|T Y U S .---------P--. D C E A|H|O M L I . . . . . .----H-------. .-T-. A C|D|E . . . . . . . . . . .--D--. .----O S U-. |A|C . . . . . . . . . . . . A-. E I---. Y .|C|. . . . . . . . . . . . C .-M . . .|E|. . . . . . . . . . L . . . . . I M L|O|. . . . . . . . . .|I|M L . . . . . . . . . . . . L|M|. . . . . . . . . . . .|L|. . . . . . . . . . . . . . . . . S|T|U Y . . . . . . . . . .|S|. . . . . . . . . . . . . . .|U|Y . . . . . . . . . . . . .|Y| A C D E H I L M O P S T U Y
Remark: Correspondence is 1–1 if array has no duplicate keys
correspondence: BSTs and QS partitioning
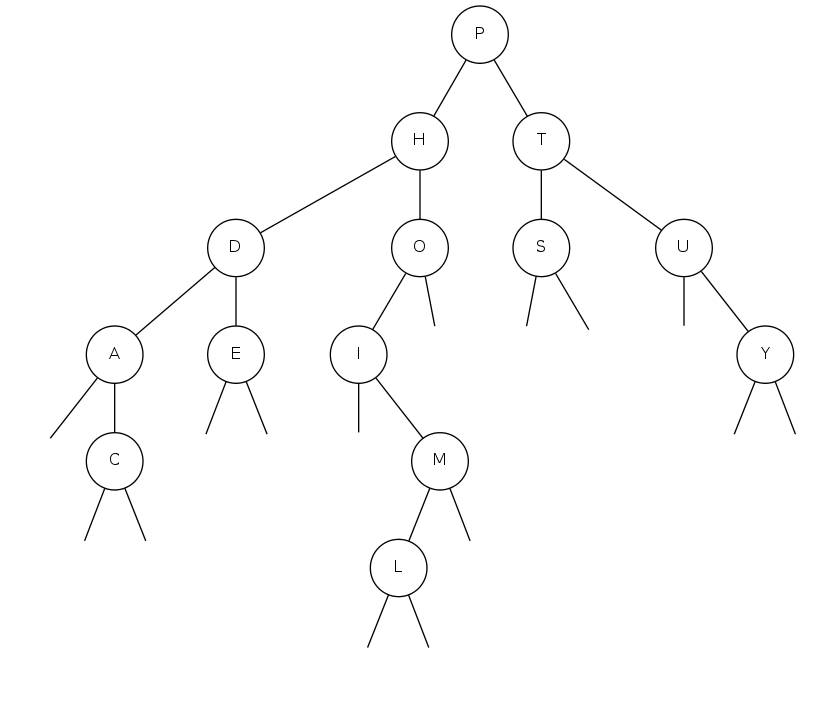
Remark: Correspondence is 1–1 if array has no duplicate keys
BSTs: mathematical analysis
Proposition: If \(N\) distinct eys are inserted into a BST in random order, the expected number of compares for a search/insert is \(\texttilde 2\ln N\).
Pf: 1–1 correspondence with quicksort partitioning
Proposition [Reed, 2003]: If \(N\) distinct keys are inserted into a BST in random order, the expected height is \(\texttilde 4.311 \ln N\) (expected depth of function-call stack in quicksort)
But... Worst-case height is \(N-1\) (exponentially small chance when keys are inserted in random order)
ST implementations: summary
| implementation | search\(^*\) | insert\(^*\) | search\(^\dagger\) | insert\(^\dagger\) | ops on keys |
|---|---|---|---|---|---|
| seq search (unordered list) | \(N\) | \(N\) | \(N\) | \(N\) | equals() |
| binary search (ordered array) | \(\log N\) | \(N\) | \(\log N\) | \(N\) | compareTo() |
| BST | \(N\) | \(N\) | \(\log N\) | \(\log N\) | compareTo() |
\(^*\)guarantee, \(^\dagger\)average
Why not shuffle to ensure a (probabilistic) guarantee of \(\log N\)?
Binary search trees
ordered operations
minimum and maximum
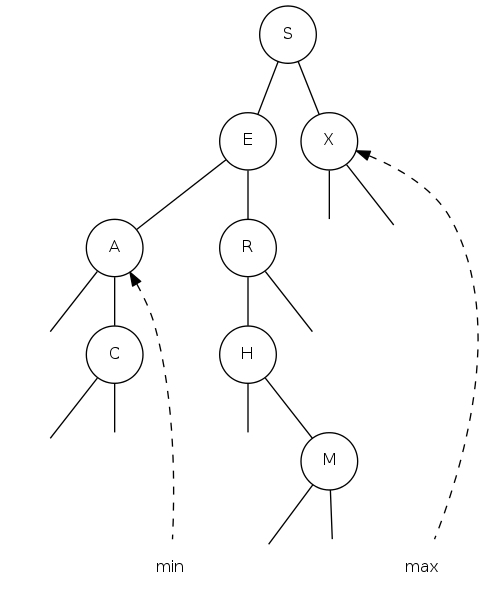
|
Minimum: Smallest key in table Maximum: largest key in table Q. How to find the min / max? |
 |
floor and ceiling
|
Floor: Largest key \(\leq\) a given key Ceiling: Smallest key \(\geq\) a given key Q. How to find the floor / ceiling? |
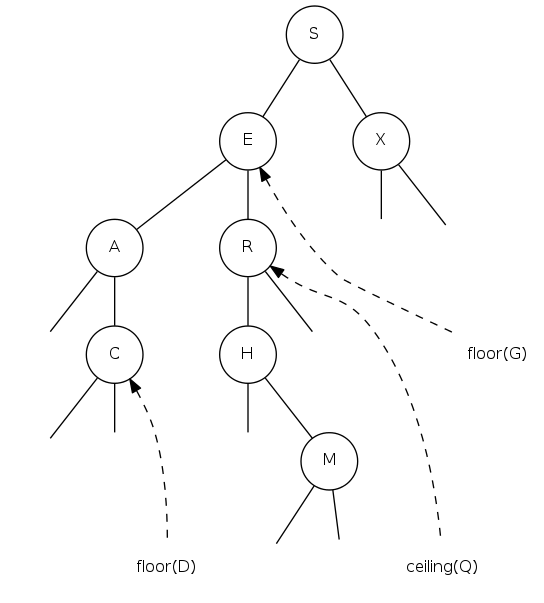 |
computing the floor
Floor: Find largest key \(\leq k\)
Three cases:
- key in node \(x = k\): the floor of \(k\) is \(k\)
- key in node \(x > kP\): the floor of \(k\) is in the left subtree of \(x\)
- key in node \(x < k\): the floor of \(k\) can't be in left subtree of \(x\), so it is either in the right subtree of \(x\) or it is the key in node \(x\)
Challenge: Prove to yourself that the above is correct.
computing the floor
public Key floor(Key key) {
Node x = floor(root, key);
if(x == null) return null;
return x.key;
}
private Node floor(Node x, Key key) {
if(x == null) return null;
int cmp = key.compareTo(x.key);
if(cmp == 0) return x;
if(cmp < 0) return floor(x.left, key);
Node t = floor(x.right, key);
if(t != null) return t;
else return x;
}
rank and select
Q. How to implement rank() and select() efficiently?
A. In each node, store the number of nodes in its subtree
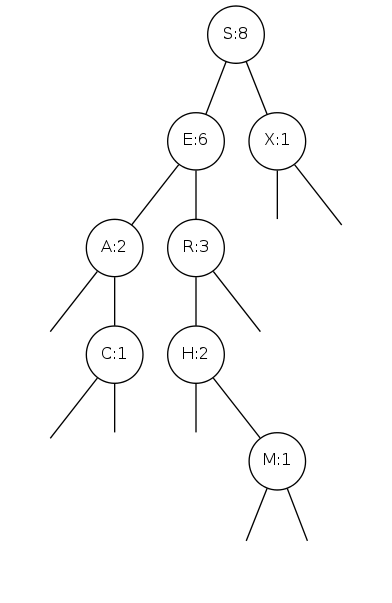
Number in node represents count of nodes in subtree rooted at node
BST implementation: subtree counts
public class BST<Key extends Comparable<Key>, Value> {
private Node root;
private class Node {
/* ... */
private int count; // number of nodes in subtree
private Node put(Node x, Key key, Value val) {
if(x == null) {
// init subtree count to 1
return new Node(key, val, 1);
}
int cmp = key.compareTo(x.key);
if (cmp < 0) x.left = put(x.left, key, val);
else if(cmp > 0) x.right = put(x.right, key, val);
else x.val = val;
x.count = 1 + size(x.left) + size(x.right);
return x;
}
}
public int size() { return size(root); }
private int size(Node x) {
if(x == null) return 0; // ok to call when x is null
return x.count;
}
}
computing the rank
Rank: How many keys \(< k\)?
Three cases:
- key in node \(x = k\): All keys in left subtree \(< k\); no key in right subtree \(< k\)
- key in node \(x > k\): No key in right subtree \(< k\); recursively compute rank in left subtree
- key in node \(X < k\): All keys in left subtree \(< k\); some keys in right subtree may be \(< k\)
Easy recursive algorithm (3 cases)
rank
public int rank(Key key) { return rank(key, root); }
private int rank(Key key, Node x) {
if(x == null) return 0;
int cmp = key.compareTo(x.key);
if (cmp < 0) return rank(key, x.left);
else if(cmp > 0) return 1 + size(x.left) + rank(key, x.right);
else return size(x.left);
}
symbol table operations summary
| sequential search | binary search | BST | |
|---|---|---|---|
| search | \(N\) | \(\log N\) | \(h\) |
| insert | \(N\) | \(N\) | \(h\) |
| min / max | \(N\) | \(1\) | \(h\) |
| floor / ceiling | \(N\) | \(\log N\) | \(h\) |
| rank | \(N\) | \(\log N\) | \(h\) |
| select | \(N\) | \(1\) | \(h\) |
| ordered iteration | \(N \log N\) | \(N\) | \(N\) |
where \(h\) is height of BST (proportional to \(\log N\) if keys inserted in random order)
binary search trees
deletion
ST implementation: summary
| implementation | search\(^*\) | insert\(^*\) | delete\(^*\) | search\(^\dagger\) | insert\(^\dagger\) | delete\(^\dagger\) | ops on keys |
|---|---|---|---|---|---|---|---|
| seq search (unordered list) | \(N\) | \(N\) | \(N\) | \(N\) | \(N\) | \(N\) | equals() |
| binary search (ordered array) | \(\log N\) | \(N\) | \(N\) | \(\log N\) | \(N\) | \(N\) | compareTo() |
| BST | \(N\) | \(N\) | \(N\) | \(\log N\) | \(\log N\) | ? | compareTo() |
\(^*\)guarantee, \(^\dagger\)average
Next: Deletion in BSTs
bst deletion: lazy approach
To remove a node with a given key:
- Set its value to
null - Leave key in tree to guide search (but don't consider it equal in search)
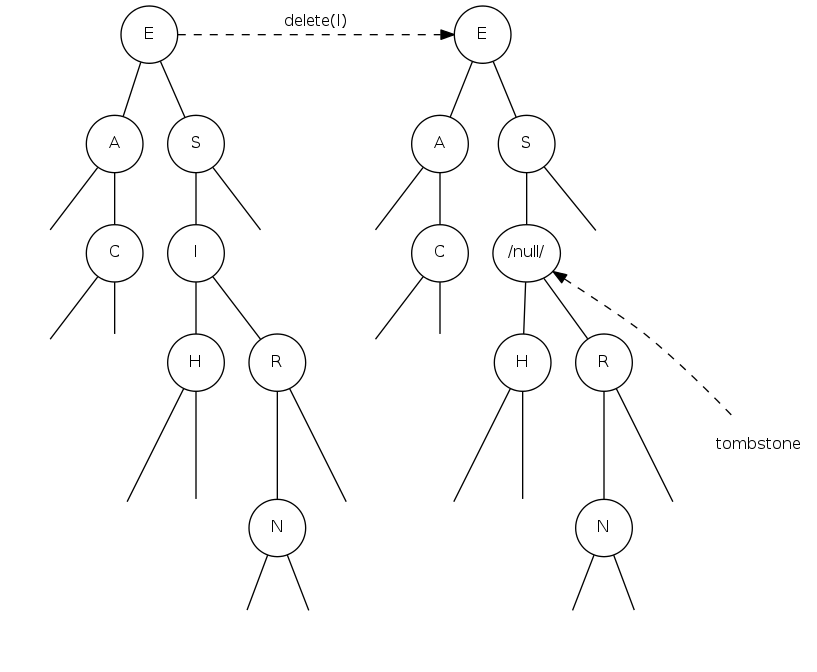
bst deletion: lazy approach
Cost: \(\texttilde 2 \ln N'\) per insert, search, and delete (if keys in random order), where \(N'\) is the number of key-value pairs ever inserted in the BST.
Unsatisfactory solution: tombstone (memory) overload
deleting the minimum
To delete the minimum key:
- Go left until finding a node with a
nullleft link - Replace that node by its right link
- Update subtree counts
public void deleteMin() {
root = deleteMin(root);
}
private Node deleteMin(Node x) {
if(x.left == null) return x.right;
x.left = deleteMin(x.left);
x.count = 1 + size(x.left) + size(x.right);
return x;
}
Challenge: Prove to yourself that the above is correct.
hibbard deletion
To delet a node with key k: search for node t containing key k.
- 0 children: delete
tby setting parent link tonull - 1 child: delete
tby replacing parent link - 2 children:
- find successor
xoft(xhas no left child) - delete the minimum in
t's right subtree (but don't garbage collectx) - put
xint's spot (still a BST)
- find successor
hibbard deletion: java implementation
public void delete(Key key) {
root = delete(root, key);
}
private Node delete(Node x, Key key) {
if(x == null) return null;
// search for key
int cmp = key.compareTo(x.key);
if (cmp < 0) x.left = delete(x.left, key);
else if(cmp > 0) x.right = delete(x.right, key);
else {
if(x.right == null) return x.left; // no right child
if(x.left == null) return x.right; // no left child
// replace with successor
Node t = x;
x = min(t.right);
x.right = deleteMin(t.right);
x.left = t.left;
}
// update subtree counts
x.count = size(x.left) + size(x.right) + 1;
return x;
}
hibbard deletion: analysis
Unsatisfactory solution: not symmetric
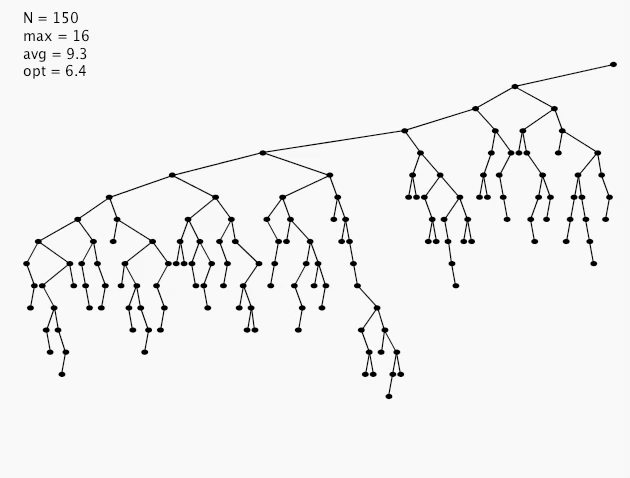
Surprising consequence: Trees not random (!) \(\Rightarrow \sqrt{N}\) per op
Longstanding open problem: Simple and efficient delete for BSTs
ST implementation: summary
| implementation | search\(^*\) | insert\(^*\) | delete\(^*\) | search\(^\dagger\) | insert\(^\dagger\) | delete\(^\dagger\) | ops on keys |
|---|---|---|---|---|---|---|---|
| seq search (unordered list) | \(N\) | \(N\) | \(N\) | \(N\) | \(N\) | \(N\) | equals() |
| binary search (ordered array) | \(\log N\) | \(N\) | \(N\) | \(\log N\) | \(N\) | \(N\) | compareTo() |
| BST | \(N\) | \(N\) | \(N\) | \(\log N\) | \(\log N\) | \(\sqrtN\) | compareTo() |
\(^*\)guarantee, \(^\dagger\)average
Average case for other BST operations also become \(\sqrt{N}\) if deletions allowed
Next: Guarantee logarithmic performance for all operations
