Symbol Tables
COS 265 - Data Structures & Algorithms
Data Structures
“Smart data structures and dumb code works a lot better than the other way around.
”
—Eric S. Raymond
Symbol Tables
API
symbol tables
Key-value pair abstraction
- Insert a value with specified key
- Given a key, search for the corresponding value
Ex: DNS Lookup
- Insert domain name (key) with specified IP address (value)
- Given domain name, find corresponding IP address
| domain name | IP address |
|---|---|
| cse.taylor.edu | 192.195.249.26 |
| gfx.cse.taylor.edu | 192.195.249.31 |
| taylor.edu | 192.195.250.21 |
symbol table applications
| application | purpose of search | key | value |
|---|---|---|---|
| dictionary | find definition | word | definition |
| book index | find relevant pages | term | list of page numbers |
| file share | find song to download | name of song | computer ID |
| financial account | process transactions | account number | transaction details |
| web search | find relevant web pages | keyword | list of page names |
| compiler | find properties of variables | variable name | type and value |
| routing table | route Internet packets | destination | best route |
| DNS | find IP address | domain name | IP address |
| reverse DNS | find domain name | IP address | domain name |
| genomics | find markers | DNA string | known positions |
| file system | find file on disk | filename | location on disk |
symbol tables: context
Also known as: maps, dictionaries, associative arrays
Generalizes arrays: Keys need not be between \(0\) and \(N-1\)
Language support
- External libraries: C, VisualBasic, Standard ML, bash, ...
- Built-in libraries: Java, C#, C++, Scala, ...
- Built-in to language: Awk, Perl, PHP, Tcl, JavaScript, Python, Ruby, Lua, ...
PHP: every array is an associative array
JavaScript: every object is an associative array
Lua: table is the only primitive data structure
hasNiceSyntaxForAssociativeArrays['Python'] = True hasNiceSyntaxForAssociativeArrays['Java'] = False # legal Python code
Basic symbol table API
Associative array abstraction: associate one value with each key
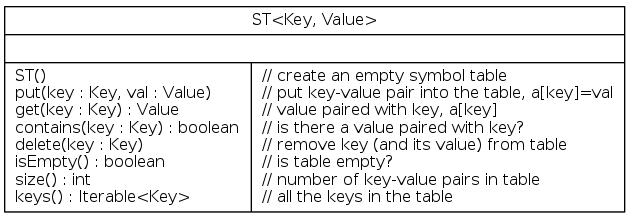
conventions
- Values are not
null(Java allowsnullvalue) - Method
get()returnsnullif key not present - Method
put()overwrites old value with new value
Intended consequences
- Easy to implement
contains()
public boolean contains(Key key) {
return get(key) != null;
}
- Can implement lazy version of
delete()
public void delete(Key key) {
put(key, null);
}
keys and values
Value type: any generic type
Key type: several natural assumptions
- Assume keys are
Comparable, usecompareTo()(specifyComparablein API) - Assume keys are any generic type, use
equals()to test equality- use
hashCode()to scramble key - built-in to Java (stay tuned)
- use
Best practices: Use immutable types for symbol table keys
- Immutable in Java:
Integer,Double,String, ... - Mutable in Java:
StringBuilder, arrays, ...
equality test
All java classes inherit a method equals()
Java requirements: for any references x, y, and z:
- Reflexive:
x.equals(x)istrue - Symmetric:
x.equals(y)iffy.equals(x) - Transitive: if
x.equals(y)andy.equals(z), thenx.equals(z) - Non-null:
x.equals(null)isfalse
Equivalence relation: reflexive, symmetric, transitive
Default implementation: (x==y: do x and y refer to same object?)
Customized implementations: Integer, Double, String, ...
User-defined implementations: some care needed
implementing equals for user-defined types
Seems easy
public class Date implements Comparable<Date> {
private final int month;
private final int day;
private final int year;
/* ... */
public boolean equals(Date that) {
// check that all significant fields are the same
if(this.day != that.day ) return false;
if(this.month != that.month) return false;
if(this.year != that.year ) return false;
return true;
}
}
implementing equals for user-defined types
Seems easy, but requires some care
// typically unsafe to use equals() with inheritance
// (would violate symmetry)
public final class Date implements Comparable<Date> {
private final int month;
private final int day;
private final int year;
/* ... */
// must be Object (why? experts still debate)
public boolean equals(Object y) {
// optimize for true object equality
if(y == this) return true;
// check for null
if(y == null) return false;
// objects must be in the same class
// (religion: getClass() vs instanceof)
if(y.getClass() != this.getClass()) return false;
// cast is guaranteed to succeed
Date that = (Date) y;
// check that all significant fields are the same
if(this.day != that.day ) return false;
if(this.month != that.month) return false;
if(this.year != that.year ) return false;
return true;
}
}
equals design
"Standard" recipe for user-defined types
- Optimization for reference equality
- Check against
null - Check that two objects are of the same type; cast
- Compare each significant field:
- if field is a primitive type, use
==(but useDouble.compare()withdoubleto deal with-0.0andNaN) - if field is an object, use
equals()(apply rule recursively) - if field is an array, apply to each entry (can use
Arrays.deepEquals(a,b)but nota.equals(b))
- if field is a primitive type, use
equals design
Best practices
- No need to use calculated fields that depend on other fields
- Compare fields mostly likely to differ first
- Make
compareTo()consistent withequals()(x.equals(y)iffx.compareTo(y) == 0)
ST test client for traces
Build ST by associating value i with ith string from standard input
public static void main(String[] args) {
ST<String, Integer> st = new ST<String, Integer>();
for(int i = 0; !StdIn.isEmpty(); i++) {
String key = StdIn.readString();
st.put(key, i);
StdOut.print(s + " " + i + ", ");
}
StdOut.println();
for(String s : st.keys())
StdOut.print(s + " " + st.get(s) + ", ");
StdOut.println();
}
$ java STTestClient < searchexample.txt S 0, E 1, A 2, R 3, C 4, H 5, E 6, X 7, A 8, M 9, P 10, L 11, E 12, A 8, C 4, E 12, H 5, L 11, M 9, P 10, R 3, S 0, X 7,
st test client for analysis
Frequency counter: Read a sequence of strings from standard input and print out one that occurs with highest frequency
$ cat tinyTale.txt it was the best of times it was the worst of times it was the age of wisdom it was the age of foolishness it was the epoch of belief it was the epoch of incredulity it was the season of light it was the season of darkness it was the spring of hope it was the winter of despair $ # tiny example (60 words, 20 distinct) $ java FrequencyCounter 1 < tinyTale.txt it 10 $ # real example (135,635 words, 10,769 distinct) $ java FrequencyCounter 8 < tale.txt business 122 $ # real example (21,191,455 words, 534,580 distinct) $ java FrequencyCounter 10 < leipzip1M.txt government 24763
frequency counter implementation
public class FrequencyCounter {
public static void main(String[] args) {
int minlen = Integer.parseInt(args[0]);
ST<String, Integer> st = new ST<>(); // create ST
while(!StdIn.isEmpty()) {
// read string and update frequency
String word = StdIn.readString();
if(word.length() < minlen) continue; // ignore short str
if(!st.contains(word)) st.put(word, 1);
else st.put(word, st.get(word) + 1);
}
// print a string with max freq
String max = "";
st.put(max, 0);
for(String word : st.keys())
if(st.get(word) > st.get(max)) max = word;
StdOut.println(max + " " + st.get(max));
}
}
symbol tables
elementary implementations
sequential search in a linked list
Data structure: Maintain an (unordered) linked list of key-value pairs
Search: Scan through all keys until find a match
Insert: Scan through all keys until find a match; if no match add to front
k v first - -- ----- S 0 S,0 E 1 E,1 > S,0 A 2 A,2 > E,1 > S,0 R 3 R,3 > A,2 > E,1 > S,0 C 4 C,4 > R,3 > A,2 > E,1 > S,0 H 5 H,5 > C,4 > R,3 > A,2 > E,1 > S,0 E 6 H,5 > C,4 > R,3 > A,2 > E,6 > ... X 7 X,7 > H,5 > C,4 > R,3 > A,2 > E,1 > S,0 A 8 X,7 > H,5 > C,4 > R,3 > A,8 > ... M 9 M,9 > X,7 > H,5 > C,4 > R,3 > A,2 > E,1 > S,0 P 10 P,10 > M,9 > X,7 > H,5 > C,4 > R,3 > A,2 > E,1 > S,0 L 11 L,11 > P,10 > M,9 > X,7 > H,5 > C,4 > R,3 > A,2 > E,1 > S,0 E 12 L,11 > P,10 > M,9 > X,7 > H,5 > C,4 > R,3 > A,2 > E,12 > ...
elementary ST implementations: summary
| implementation | search\(^*\) | insert\(^*\) | search\(^\dagger\) | insert\(^\dagger\) | ops on keys |
|---|---|---|---|---|---|
| seq search (unordered list) | \(N\) | \(N\) | \(N\) | \(N\) | equals() |
\(^*\)guarantee, \(^\dagger\)average
Challenge: Efficient implementations of both search and insert
binary search in an ordered array
Data structure: Maintain an ordered array of key-value pairs
Rank helper function: How many keys < key?
0 1 2 3 4 5 6 7 8 9 keys[] = A C E H L M P R S X lo hi m successful search for P 0 9 4 A C E H L M P R S X 5 9 7 . . . . . M P R S X 5 6 5 . . . . . M P . . . 6 6 6 . . . . . . P . . . loop exist with keys[m] = P: return 6 lo hi m unsuccessful search for Q 0 9 4 A C E H L M P R S X 5 9 7 . . . . . M P R S X 5 6 5 . . . . . M P . . . 7 6 6 . . . . . . P . . . loop exits with lo > hi: return 7
binary search: java implementation
public Value get(Key key) {
if(isEmpty()) return null;
int i = rank(key);
if(i < N && keys[i].compareTo(key) == 0) return vals[i];
else return null;
}
// find number of keys < key
private int rank(Key key) {
int lo = 0; int hi = N-1;
while(lo <= hi) {
int mid = lo + (hi - lo) / 2;
int cmp = key.compareTo(keys[mid]);
if (cmp < 0) hi = mid - 1;
else if(cmp > 0) lo = mid + 1;
else return mid;
}
return lo;
}
elementary symbol tables: quiz 1
Implementing binary search was
A. Easier that I thought
B. About what I expected
C. Harder than I thought
D. Much harder than I thought
E. I don't know (well, you should!)
Exercise: Find the first 1
Problem: Given an array with all 0s in the beginning and all 1s at the end, find the index in the array where the 1s start.
Input: 000000 ... 0000111111 ... 1111
Variant 1: You are given the length of the array
Variant 2: You are not given the length of the array
binary search: trace of indexing client
Problem: To insert, need to shift all greater keys over
k v keys[] N vals[]
- -- ------------------- --- -----------------------------
S 0 S 1 0
E 1 E S 2 1 0
A 2 A E S 3 2 1 0
R 3 . . R S 4 . . 3 0
C 4 . C E R S 5 . 4 1 3 0
H 5 . . . H R S 6 . . . 5 3 0
E 6 . . . . . . 6 . . 6 . . .
X 7 . . . . . . X 7 . . . . . . 7
A 8 . . . . . . . 7 8 . . . . . .
M 9 . . . . M R S X 8 . . . . 9 3 0 7
P 10 . . . . . P R S X 9 . . . . . 10 3 0 7
L 11 . . . . L M P R S X 10 . . . . 11 9 10 3 0 7
E 12 . . . . . . . . . . 11 . . 12 . . . . . . .
A C E H L M P R S X 8 4 12 5 11 9 10 3 0 7
elementary ST implementations: summary
| implementation | search\(^*\) | insert\(^*\) | search\(^\dagger\) | insert\(^\dagger\) | ops on keys |
|---|---|---|---|---|---|
| seq search (unordered list) | \(N\) | \(N\) | \(N\) | \(N\) | equals() |
| binary search (ordered array) | \(\log N\) | \(N\) | \(\log N\) | \(N\) | compareTo() |
\(^*\)guarantee, \(^\dagger\)average
Challenge: Efficient implementations of both search and insert
Symbol Tables
Ordered operations
examples of ordered symbol table API
| keys | values | keys | values | |||
|---|---|---|---|---|---|---|
| => | 09:00:00 | Chicago | 09:19:32 | Chicago | ||
| 09:00:03 | Phoenix | 09:19:46 | Chicago | |||
| 09:00:13 | Houston | 09:21:05 | Chicago | |||
| 09:00:59 | Chicago | 09:22:43 | Seattle | |||
| 09:01:10 | Houston | 09:22:54 | Seattle | |||
| 09:03:13 | Chicago | 09:25:52 | Chicago | |||
| 09:10:11 | Seattle | 09:35:21 | Chicago | |||
| => | 09:10:25 | Seattle | 09:36:14 | Seattle | ||
| 09:14:25 | Phoenix | 09:37:44 | Phoenix | <= |
min() => 09:00:00 max() => 09:37:44 select(7) => 09:10:25 rank(09:10:25) => 7 get(09:10:25) => Seattle
examples of ordered symbol table API
| keys | values | keys | values | |||
|---|---|---|---|---|---|---|
| 09:00:00 | Chicago | 09:19:32 | Chicago | <= | ||
| 09:00:03 | Phoenix | 09:19:46 | Chicago | <= | ||
| 09:00:13 | Houston | 09:21:05 | Chicago | <= | ||
| 09:00:59 | Chicago | 09:22:43 | Seattle | <= | ||
| 09:01:10 | Houston | 09:22:54 | Seattle | <= | ||
| => | 09:03:13 | Chicago | 09:25:52 | Chicago | ||
| => | 09:10:11 | Seattle | 09:35:21 | Chicago | ||
| 09:10:25 | Seattle | 09:36:14 | Seattle | |||
| 09:14:25 | Phoenix | 09:37:44 | Phoenix |
floor(09:05:00) => 09:03:13
ceiling(09:05:00) => 09:10:11
size(09:15:00, 09:25:00) => 5
keys(09:15:00, 09:25:00) => [ 09:19:32, 09:19:46, 09:21:05,
09:22:43, 09:22:54 ]
ordered symbol table api

binary search: ordered symbol table summary
| sequential search | binary search | |
|---|---|---|
| search | \(N\) | \(\log N\) |
| insert | \(N\) | \(N\) |
| min / max | \(N\) | \(1\) |
| floor / ceiling | \(N\) | \(\log N\) |
| rank | \(N\) | \(\log N\) |
| select | \(N\) | \(1\) |
| ordered iteration | \(N \log N\) | \(N\) |
