Priority Queues

COS 265 - Data Structures & Algorithms

Priority Queues

API and Elementary Implemantions

collections

A collection is a data type that stores groups of items

data type	key operations	data structure
stack	`push`, `pop`	LL, resizing array
queue	`enqueue`, `dequeue`	LL, resizing array
priority queue	`insert`, `delete-max`	binary heap
symbol table	`put`, `get`, `delete`	BST, hash table
set	`add`, `contains`, `delete`	BST, hast table

collections

“
Show me your code and conceal your data structures, and I shall continue to be mystified. Show me your data structures, and I won't usually need your code; it'll be obvious
—Fred Brooks
”

priority queue

Collections: Insert and delete items. Which item to delete?

Stack: Remove the item most recently added
Queue: Remove the item least recently added
Randomized queue: Remove a random item
Priority queue: Remove the largest (or smallest) item

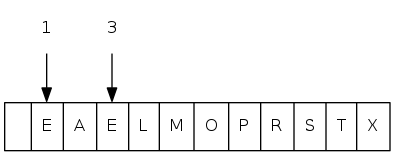
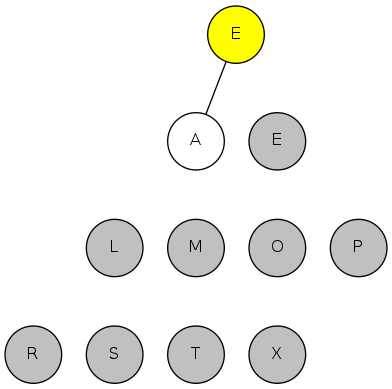
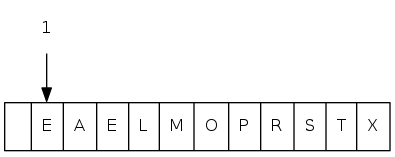
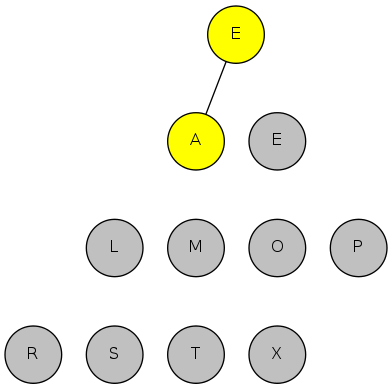
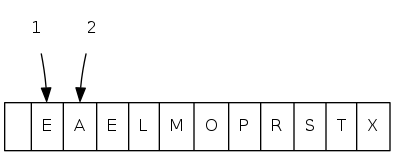
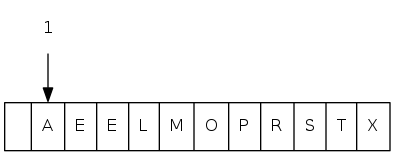
insert(P)
insert(Q)
insert(E)
remove-max() => Q
insert(X)
insert(A)
insert(M)
remove-max() => X
insert(P)
insert(L)
insert(E)
remove-max() => P

priority queue API

Requirement: Generic items are Comparable

Note: Duplicate keys allowed; delMax() and max() picks any maximum key

priority queue: applications

event-driven simulation: customers in a line, colliding particles
numerical computation: reducing roundoff error
discrete optimization: bin packing, scheduling
artificial intelligence: A* search
computer networks: web cache
operating systems: load balancing, interrupt handling
data compression: Huffman codes
graph searching: Dijkstra's algorithm, Prim's algoithm
number theory: sum of powers
spam filtering: Bayesian spam filtering
statistics: online median in data stream

priority queue: client example

Challenge: Find the largest $M$ items in a stream of $N$ items, where $N$ is huge and $M$ is large

fraud detection: isolate large $$ transactions
NSA monitoring: flag most suspicious documents

Constraint: not enough memory to store $N$ items

$ more transactions.txt
Turing      6/17/1990   644.08
vonNeumann  3/26/2002  4121.85
Dijkstra    8/22/2007  2678.40
vonNeumann  1/11/1999  4409.74
Dijkstra   11/18/1995   837.42
Hoare       5/10/1993  3229.27
vonNeumann  2/12/1994  4732.35
Hoare       8/18/1992  4381.21
Turing      1/11/2002    66.10
Thompson    2/27/2000  4747.08
Turing      2/11/1991  2156.86
Hoare       8/12/2003  1025.70
vonNeumann 10/13/1993  2520.97
Dijkstra    9/10/2000   708.95
Turing     10/12/1993  3532.36
Hoare       2/10/2005  4050.20

$ java TopM 5 < transactions.txt  # sort key = last col
Thompson    2/27/2000  4747.08
vonNeumann  2/12/1994  4732.35
vonNeumann  1/11/1999  4409.74
Hoare       8/18/1992  4381.21
vonNeumann  3/26/2002  4121.85

priority queue: client example

// Transaction data type is Comparable (ordered by $)
// use a min-oriented priority queue
MinPQ<Transaction> pq = new MinPQ<Transaction>();

while(StdIn.hasNextLine()) {
    String line = StdIn.readLine();
    Transaction transaction = new Transaction(line);
    pq.insert(transaction);
    if(pq.size() > M)
        pq.delMin();        // pq now contains largest M items
}

pq: unordered and ordered array

//                 unordered       ordered
// op     ret  sz  contents        contents
insert(P)      1   P               P
insert(Q)      2   P Q             P Q
insert(E)      3   P Q E           E P Q
delMax()   Q   2   P E             E P
insert(X)      3   P E X           E P X
insert(A)      4   P E X A         A E P X
insert(M)      5   P E X A M       A E M P X
delMax()   X   4   P E A M         A E M P
insert(P)      5   P E A M P       A E M P P
insert(L)      6   P E A M P L     A E L M P P
insert(E)      7   P E A M P L E   A E E L M P P
delMax()   P   6   E A M P L E     A E E L M P P

A sequence of operations on a priority queue that is implemented using unordered array (left) and ordered array (right)

pq: implementations cost summary

implementation	`insert`	`delMax`	`max`
unordered array	$1$	$N$	$N$
ordered array	$N$	$1$	$1$
goal for today	$\log N$	$\log N$	$\log N$

Order of growth of running time for priority queue with $N$ items

Priority Queues

Binary Heaps

complete binary tree

Binary tree: Empty or node with links to left and right binary trees

Complete tree: Perfectly balanced, except for bottom level

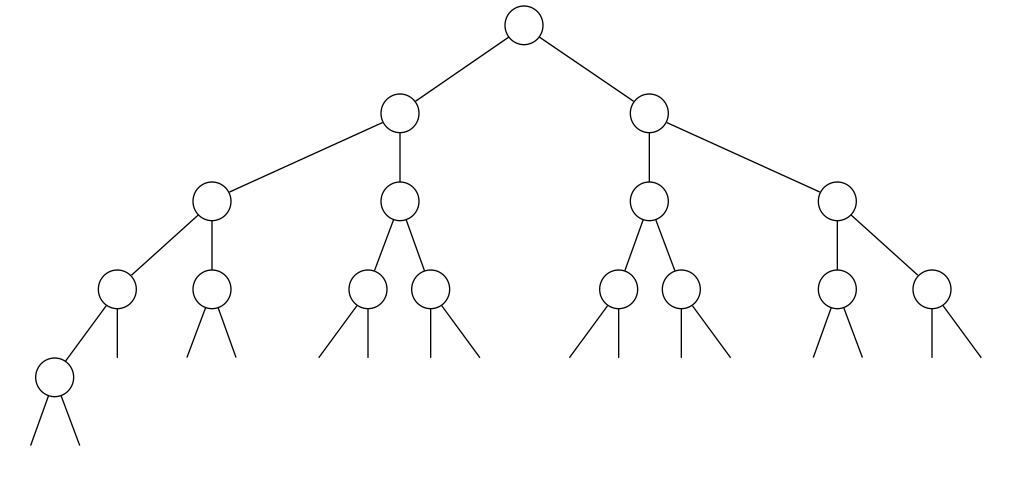
complete binary tree with $N=16 \text{ nodes}$ ($\text{height} = 4$)

Property: Height of complete binary tree with $N$ nodes is $\lfloor \lg N \rfloor$.

Pf: Height increases only when $N$ is a power of $2$.

complete binary tree in nature

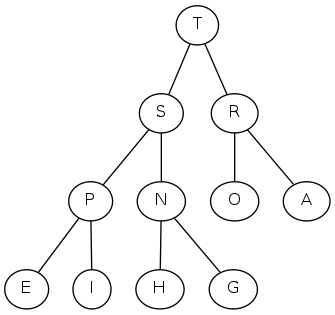
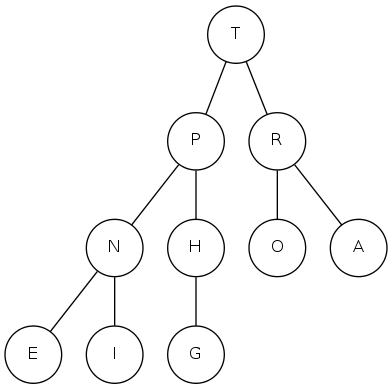
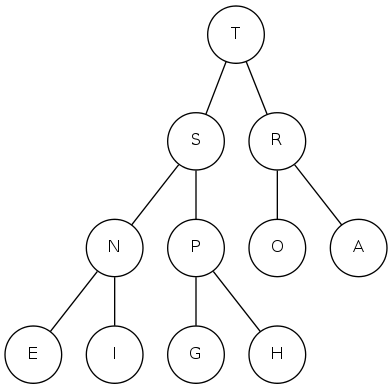
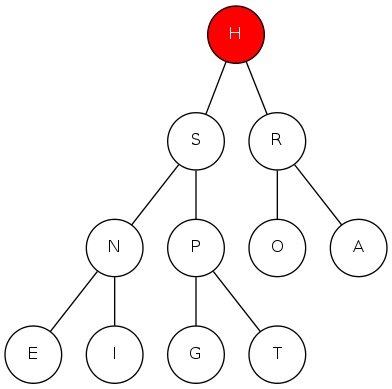
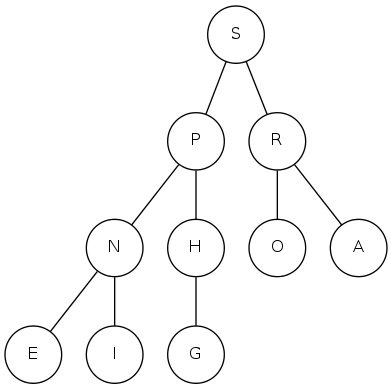
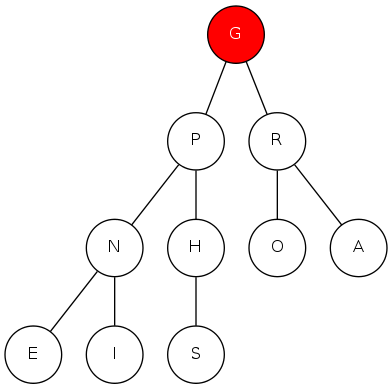
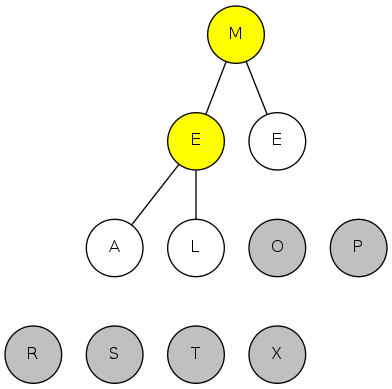
complete binary tree: array representation

Array representation

Indices start at 1
Take nodes in level order
Children of node $k$ at locations $2k$ and $2k+1$
No explicit links needed!

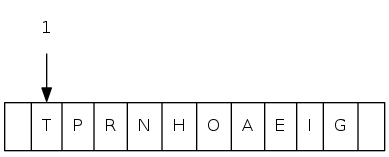
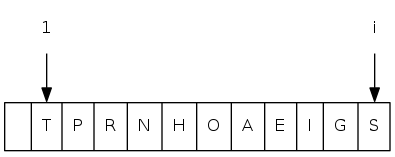
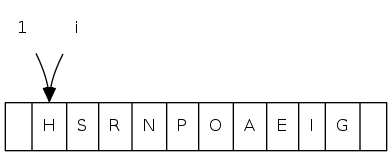
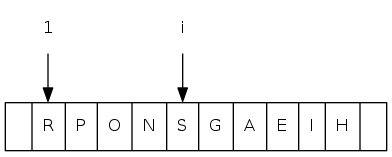
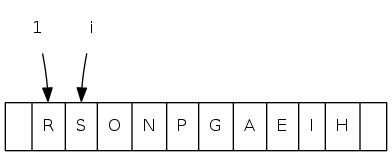
complete binary tree: array representation

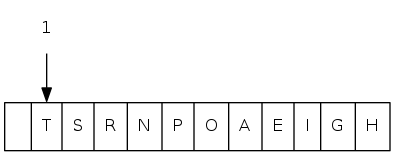
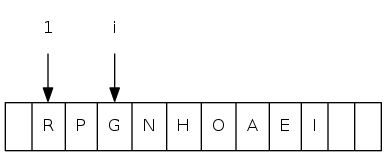
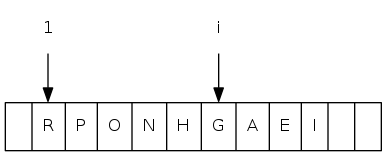
          0  1  2  3  4  5  6  7  8  9 10 11
a[i] = [  .  T  S  R  P  N  O  A  E  I  H  G]
             T
                S  R
                      P  N  O  A
                                  E  I  H  G

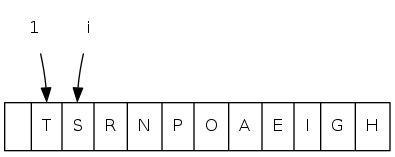
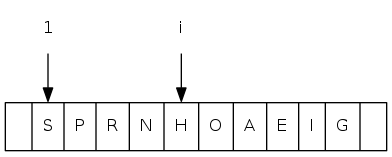
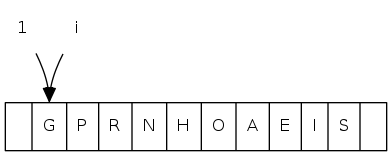
priority queues: quiz 1

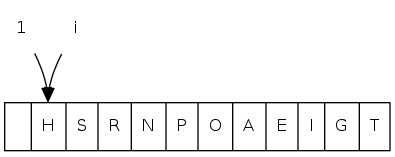
What is the index of the parent of the item at index $k$ in a binary heap?

A. $k/2 - 1$
B. $k/2$
C. $k/2 + 1$
D. None of the above
E. I don't know

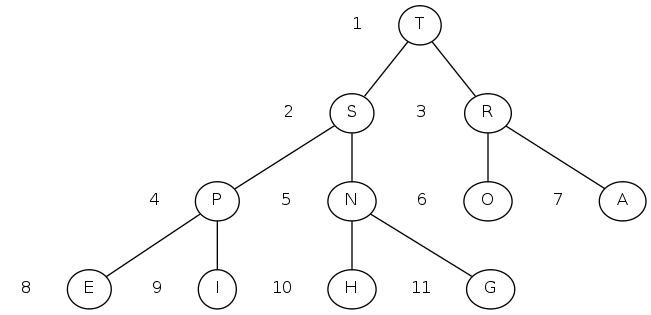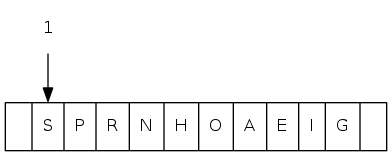
          0  1  2  3  4  5  6  7  8  9 10 11
a[i] = [  .  T  S  R  P  N  O  A  E  I  H  G]

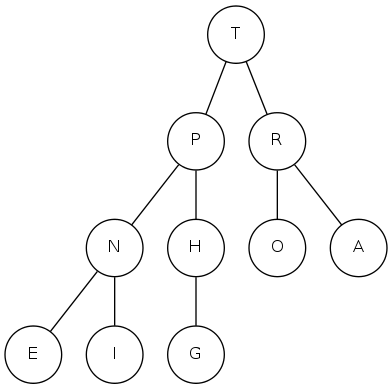
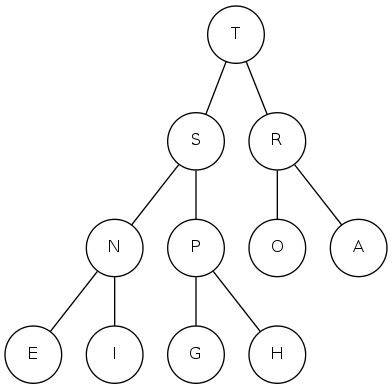
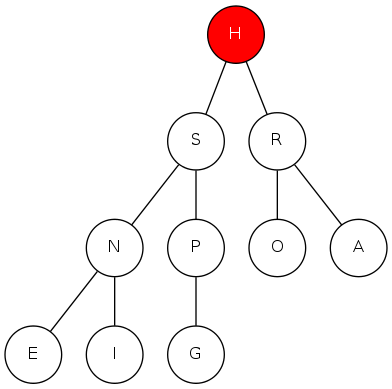
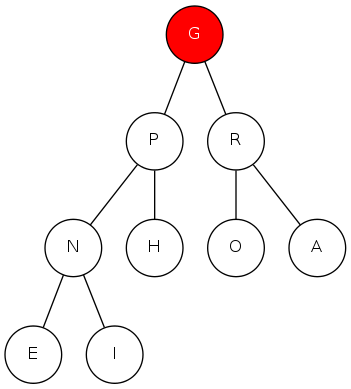
binary heap

Array representation

Indices start at 1
Take nodes in level order
Children of node $k$ at locations $2k$ and $2k+1$
No explicit links needed!

Max-Heap ordering

Keys in nodes
Parent's key no smaller than children's keys
"Just enough" ordering to support efficient priority queue operations

Binary heap: Array representation of a heap-ordered complete binary tree

binary heap: properties

"Just enough" ordering to support efficient priority queue operations.

Largest key is a[1], which is the root of the binary tree
Can use array indices to move through the tree
- Children of node at k at locations 2*k and 2*k+1
- Parent of node at k is at k/2
insert() and delMax() violate heap order, but easy to fix up

binary heap demo

Insert: Add node at end, them swim it up
Remove the maximum: Exchange root with node at end, then sink it down

binary heap demo

binary heap demo

binary heap demo

binary heap demo

binary heap demo

binary heap demo

binary heap demo

binary heap demo

binary heap demo

binary heap demo

binary heap demo

binary heap demo

binary heap demo

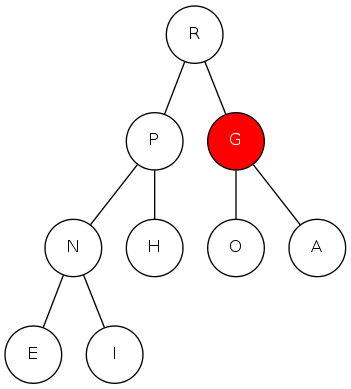
binary heap demo

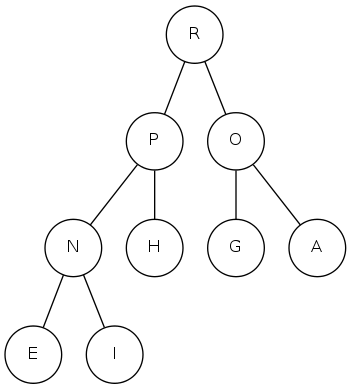
binary heap demo

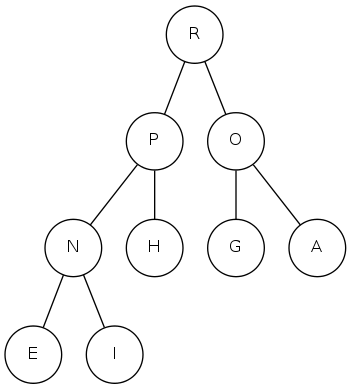
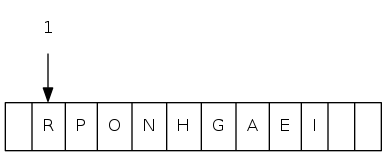
binary heap demo

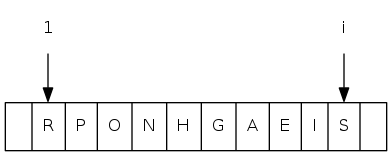
binary heap demo

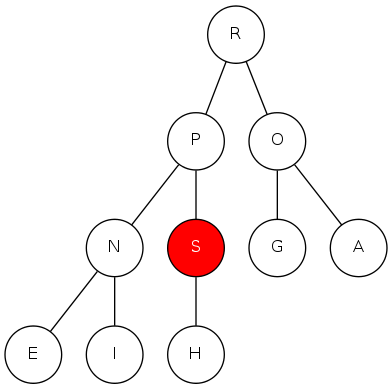
binary heap demo

binary heap demo

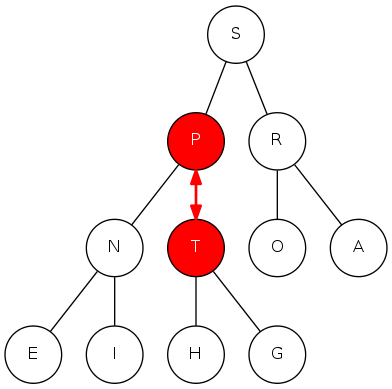
binary heap demo

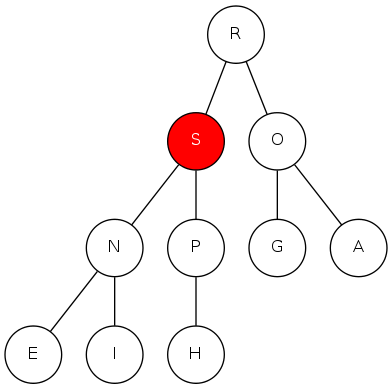
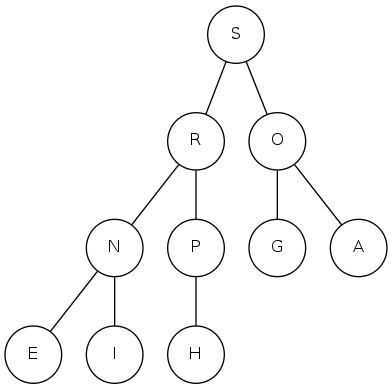
binary heap: promotion

Scenario: A key becomes larger than its parent's key

To eliminate the violation:

Exchange key in child with key in parent
Repeat until heap order restored

private void swim(int k) {
    while(k > 1 && less(k/2, k)) {
        exch(k, k/2);
        k = k/2;
    }
}

binary heap: promotion

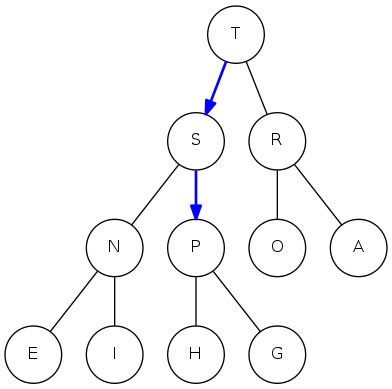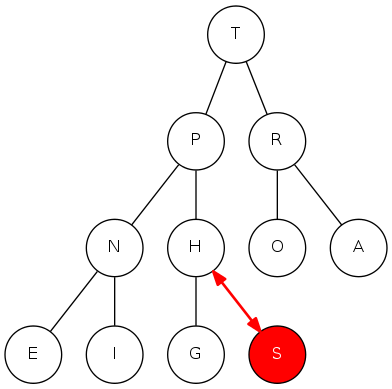
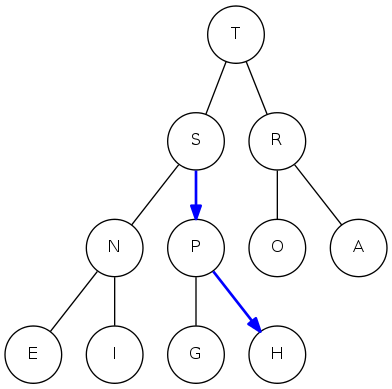
binary heap: insertion

Insert: Add node at end, then swim it up

Cost: At most $1+\lg N$ compares

public void insert(Key k) {
    pq[++N] = k;
    swim(N);
}

binary heap: insertion

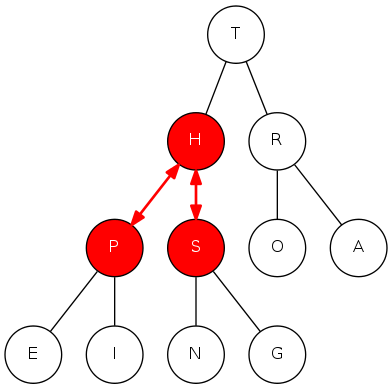
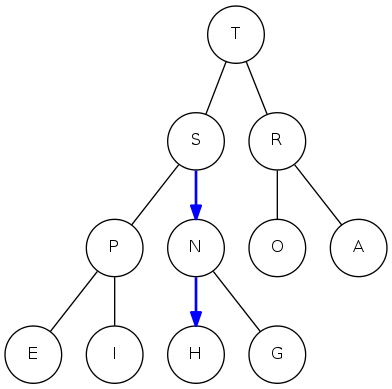
binary heap: demotion

Scenario: A key becomes smaller than one (or both) of its children's

To eliminate the violation:

Exchange key in parent with key in larger child (why not smaller child?)
Repeat until heap order is restored

private void sink(int k) {
    while(2*k <= N) {
        int j = 2*k;                    // first child
        if(j < N && less(j, j+1)) j++;  // second is larger
        if(!less(k, j)) break;          // parent > child?
        exch(k, j);
        k = j;
    }
}

binary heap: demotion

binary heap: delete the maximum

Delete max: Exchange root with node at end, then sink it down
Cost: At most $2 \lg N$ compares

public Key delMax() {
    Key max = pq[1];
    exch(1, N);
    pq[N--] = null;     // prevent loitering!
    sink(1);
    return max;
}

binary heap: delete the maximum

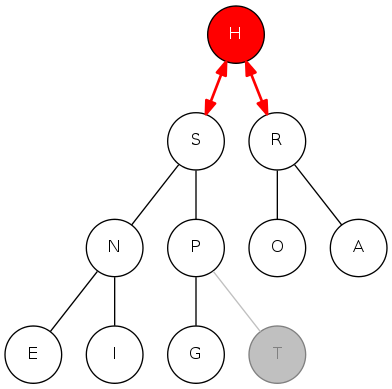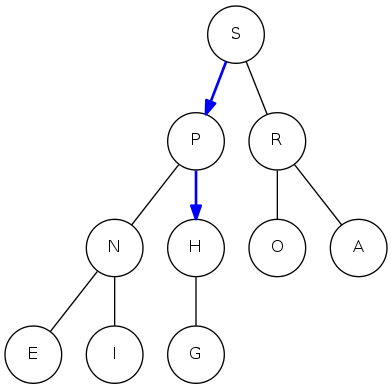binary heap: java implementation

public class MaxPQ<Key extends Comparable<Key>> {
    private Key[] pq;
    private int N;

    public MaxPQ(int capacity) {
        pq = (Key[]) new Comparable[capacity+1];
    }

    public boolean isEmpty() { return N == 0; }

    public void insert(Key key) { /* see prev code */ }
    public Key  delMax()        { /* see prev code */ }

    private void swim(int k) { /* see prev code */ }
    private void sink(int k) { /* see prev code */ }

    private boolean less(int i, int j) {
        return pq[i].compareTo(pq[j]) < 0;
    }
    private void exch(int i, int j) {
        Key t = pq[i];
        pq[i] = pq[j];
        pq[j] = t;
    }
}

pq: implementations cost summary

implementation	`insert`	`delMax`	`max`
unordered array	$1$	$N$	$N$
ordered array	$N$	$1$	$1$
binary heap	$\log N$	$\log N$	$1$

order-of-growth of running time for priority queue with $N$ items

delete-random from a binary heap

Challenge: Delete a random key from a binary heap in logarithmic time

binary heap: practical improvements

Do "half-exchanges" in sink or swim

Reduces number of array accesses
Worth doing

binary heap: practical improvements

Multiway heaps

Complete $d$-way tree
Parent's key no smaller than any of its children's keys

Fact: Height of complete $d$-way tree on $N$ nodes is $\texttilde \log_d N$

priority queues: quiz 2

How many compares (in the worst case) to insert in a $d$-way heap?

A. $\texttilde \log_2 N$

B. $\texttilde \log_d N$

C. $\texttilde d \log_2 N$

D. $\texttilde d \log_d N$

E. I don't know

priority queues: quiz 3

How many compares (in the worst case) to delete-max in a $d$-way heap?

A. $\texttilde \log_2 N$

B. $\texttilde \log_d N$

C. $\texttilde d \log_2 N$

D. $\texttilde d \log_d N$

E. I don't know

pq: implementations cost summary

implementation	`insert`	`delMax`	`max`
unordered array	$1$	$N$	$N$
ordered array	$N$	$1$	$1$
binary heap	$\log N$	$\log N$	$1$
$d$-ary heap	$\log_d N$	$d \log_d N$	$1$
Fibonacci	$1$	$\log N^*$	$1$
Brodal queue	$1$	$\log N$	$1$
impossible	$1$	$1$	$1$

$^*$ amortized
sweet spot for $d$ is $d=4$
why is last line impossible?

order-of-growth of running time for priority queue with $N$ items

binary heap: considerations

Underflow and overflow

Underflow: throw exception if deleting from empty PQ
Overflow: add no-arg constructor and use resizing array (leads to $\log N$ amortized time per op; how to make worst case?)

Minimum-oriented priority queue

Replace less() with greater()
Implement greater()

binary heap: considerations

Binary heap is not cache friendly (ex: page size = 8 nodes)

Cache-aligned $d$-heap
Funnel heap
B-heap
...

binary heap: considerations

Other operations

Remove an arbitrary item
Change the priority of an item
Can implement both efficiently with sink() and swim() (stay tuned for Prim/Dijkstra)

Immutability of keys

Assumption: client does not change keys while they're on the PQ
Best practice: use immutable keys

immutability: implementing in Java

Data type: set of values and operations on those values

Immutable data type: cannot change the data type value once created

public final class Vector {             // final = can't override
                                        // instance methods
    private final int N;                // instance vars private
    private final double[] data;        // and final

    public Vector(double[] data) {
        this.N = data.length;
        this.data = new double[N];
        for(int i = 0; i < N; i++)      // defensive copy of
            this.data[i] = data[i];     // mutable instance vars
    }

    /* ... */                           // instance methods don't
                                        // change instance vars
}

immutability: implementing in Java

Immutable: String, Integer, Double, Color, Vector, Transaction, Point2D

Mutable: StringBuilder, Stack, Counter, Java array

Advantages of immutability:

Simplifies debugging
Safer in presence of hostile code
Simplifies concurrent programming
Safe to use as key in priority queue or symbol table

Disadvantage: Must create new object for each data type value

immutability: implementing in Java

“
Classes should be immutable unless there's a very good reason to make them mutable. [...] If a class cannot be made immutable, you should still limit its mutability as much as possible.
—Joshua Bloch (Java architect)
”

[ I'm immutable t-shirt ]

Priority Queues

Heapsort

Priority queues: quiz 4

What is the name of this sorting algorithm?

public void sort(String[] a) {
    int N = a.length;
    MaxPQ<String> pq = new MaxPQ<String>();
    for(int i = 0;   i <  N; i++) pq.insert(a[i]);
    for(int i = N-1; i >= 0; i--) a[i] = pq.delMax();
}

A. insertion sort

B. mergesort

C. quicksort

D. None of the above

E. I don't know

priority queues: quiz 5

What are its properties?

public void sort(String[] a) {
    int N = a.length;
    MaxPQ<String> pq = new MaxPQ<String>();
    for(int i = 0;   i <  N; i++) pq.insert(a[i]);
    for(int i = N-1; i >= 0; i--) a[i] = pq.delMax();
}

A. $N \lg N$ compares in the worst case

B. in-place sorting

C. stable sorting

D. All of the above

E. I don't know

heapsort

Basic plan for in-place sort

View input array as a complete binary tree
Heap construction: build a max-heap with all $N$ keys
Sortdown: repeatedly remove the maximum key

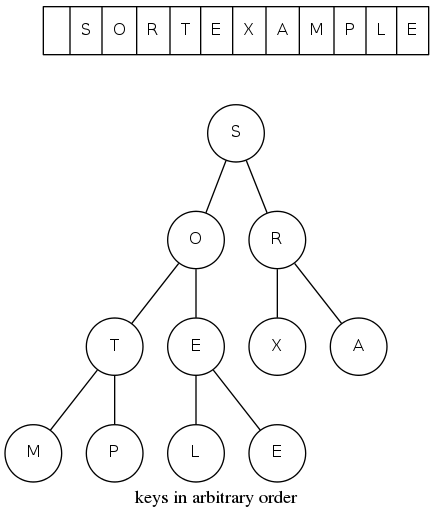
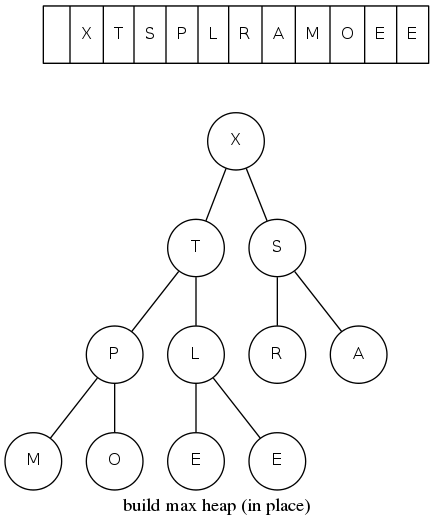
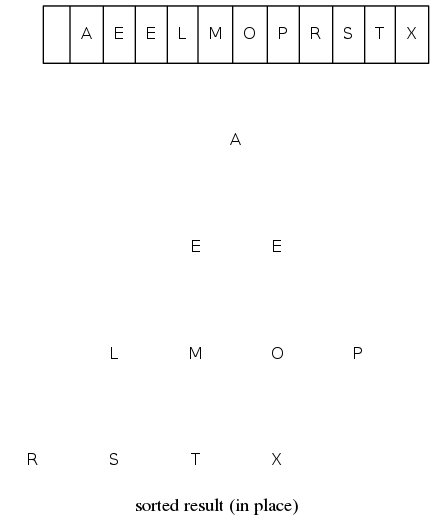
heapsort demo

Heap construction: build max heap using bottom-up method (we assume array entries are indexed 1 to N)

Sortdown: Repeatedly delete the largest remaining item

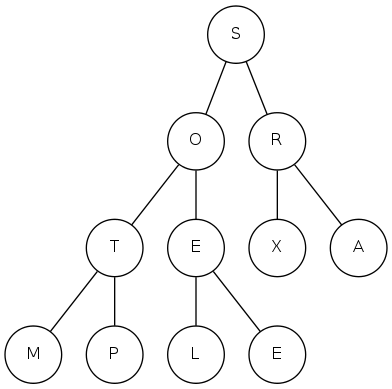
heapsort demo

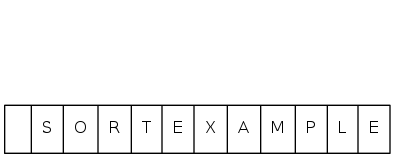
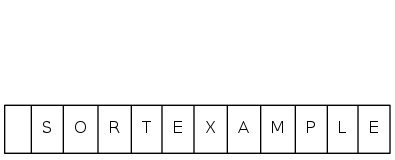
heapsort demo

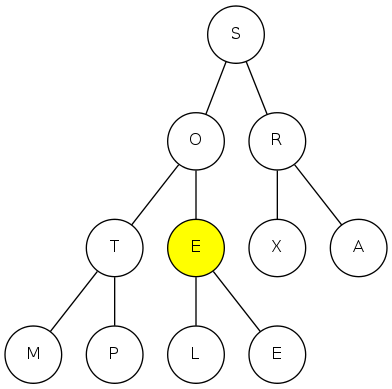
sink(5)

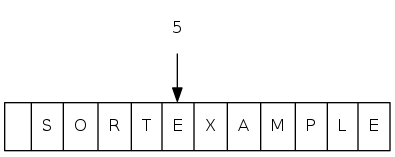
heapsort demo

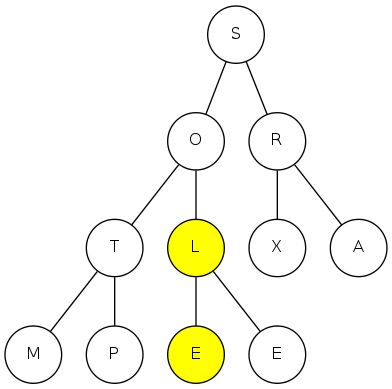
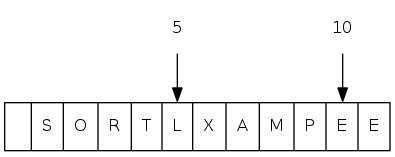
sink(5)

heapsort demo

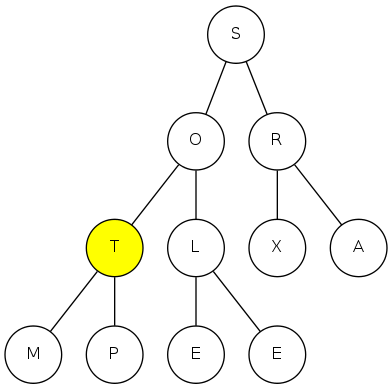
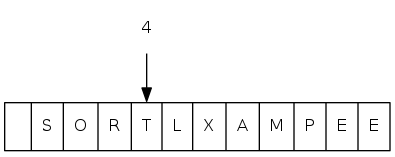
sink(4)

heapsort demo

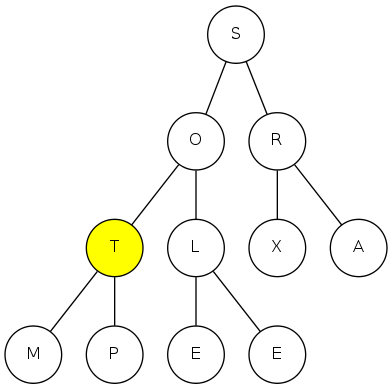
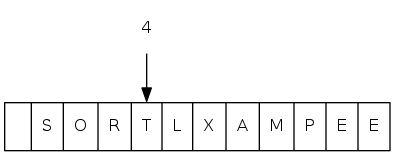
sink(4)

heapsort demo

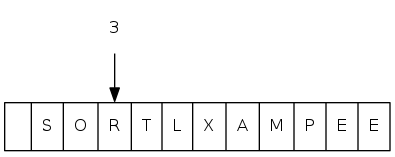
sink(3)

heapsort demo

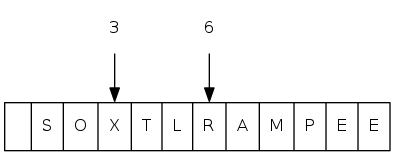
sink(3)

heapsort demo

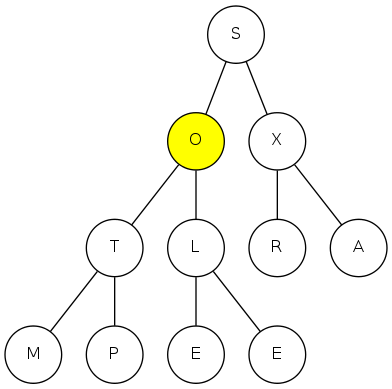
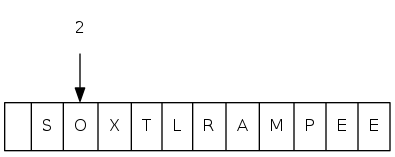
sink(2)

heapsort demo

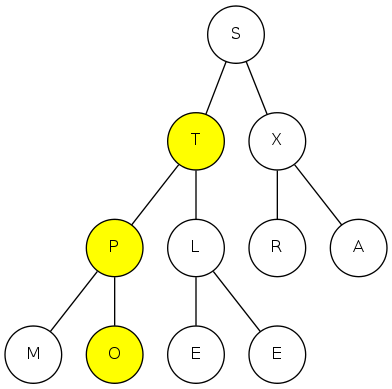
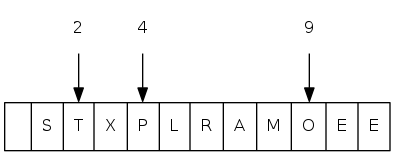
sink(2)

heapsort demo

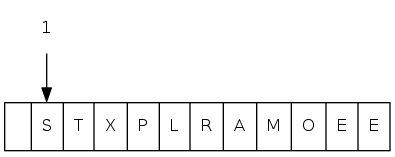
sink(1)

heapsort demo

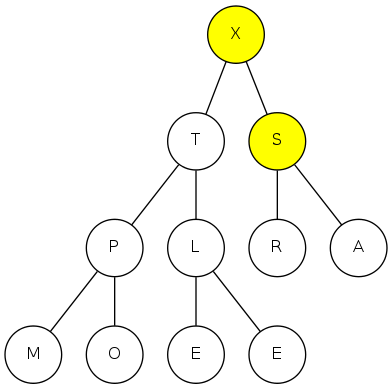
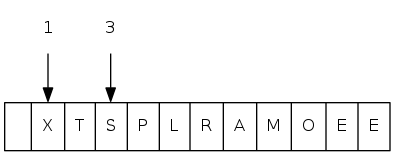
sink(1)

heapsort demo

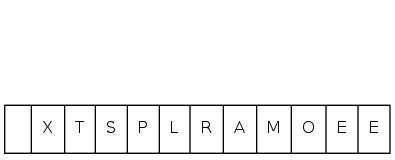
max-heap!

heapsort demo

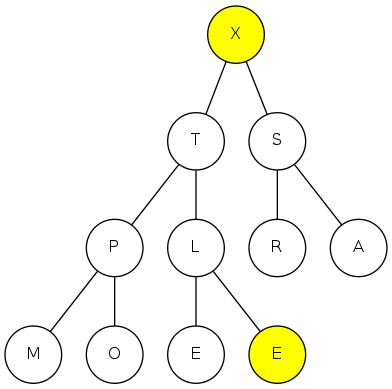
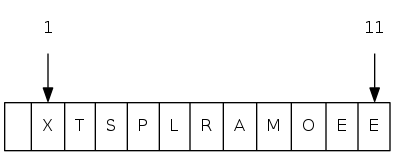
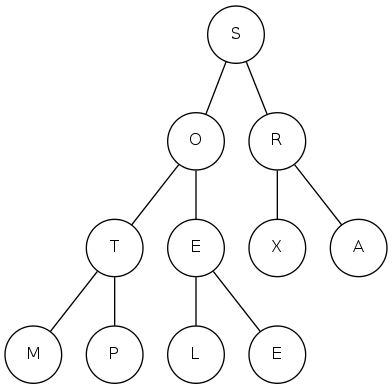
exch(11), then sink(1)

heapsort demo

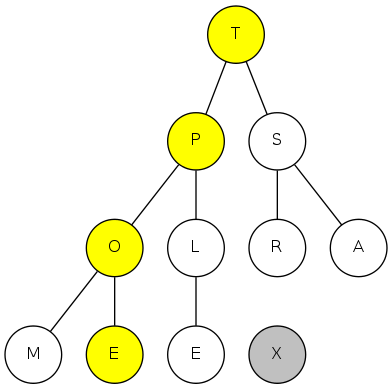
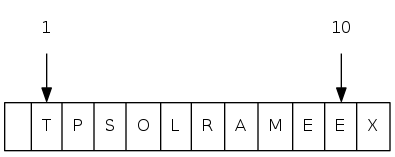
exch(10), then sink(1)

heapsort demo

exch(10), then sink(1)

heapsort demo

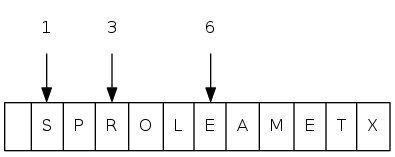
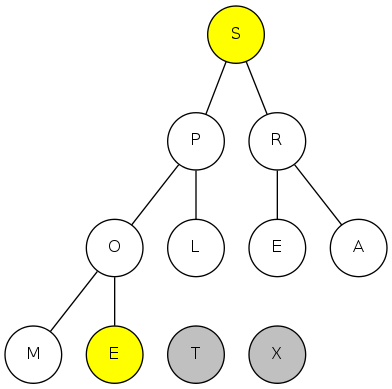
exch(9), then sink(1)

heapsort demo

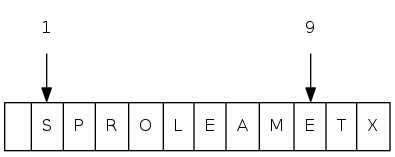
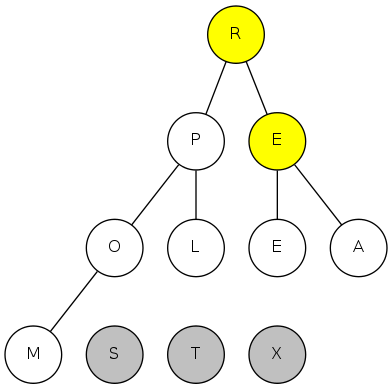
exch(9), then sink(1)

heapsort demo

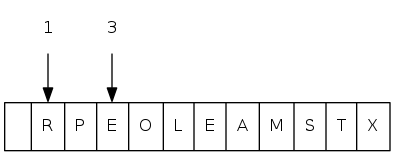
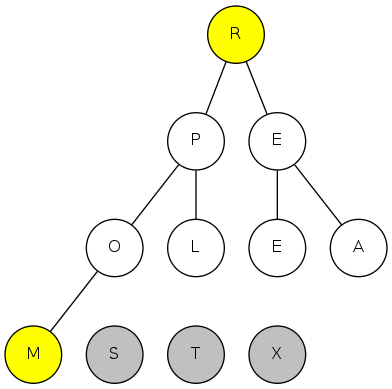
exch(8), then sink(1)

heapsort demo

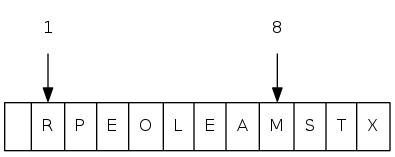
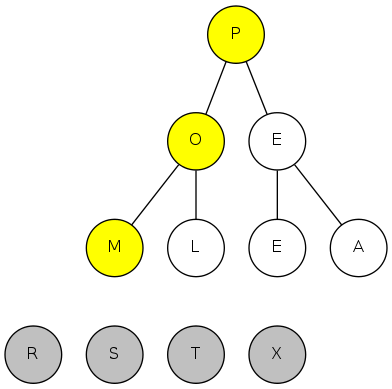
exch(8), then sink(1)

heapsort demo

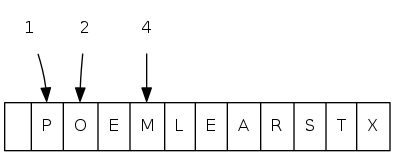
exch(7), then sink(1)

heapsort demo

exch(7), then sink(1)

heapsort demo

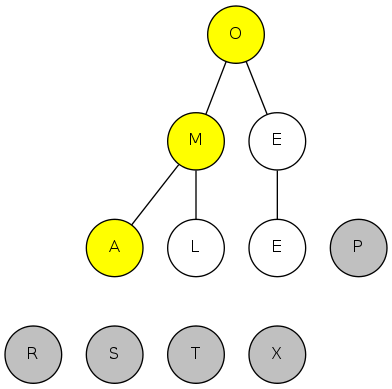
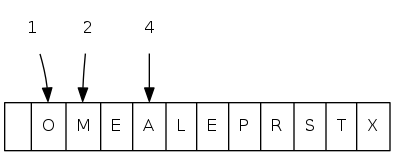
exch(6), then sink(1)

heapsort demo

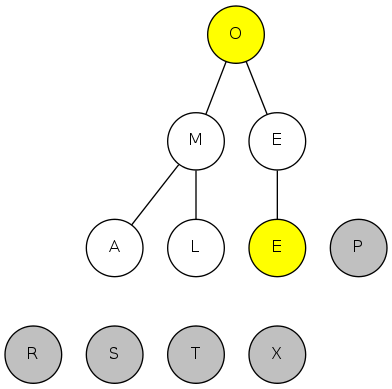
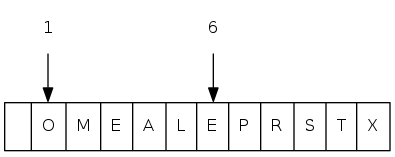
exch(6), then sink(1)

heapsort demo

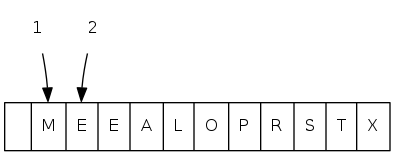
exch(5), then sink(1)

heapsort demo

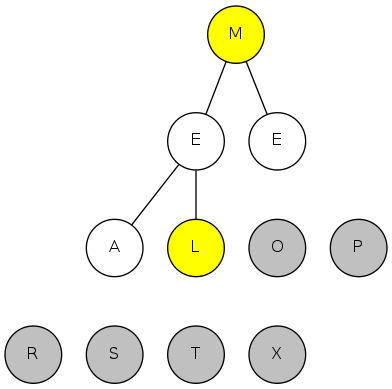
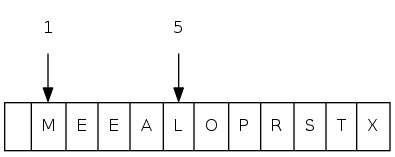
exch(5), then sink(1)

heapsort demo

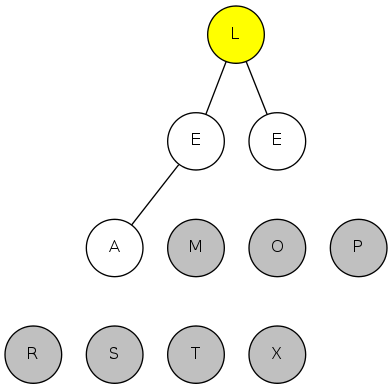
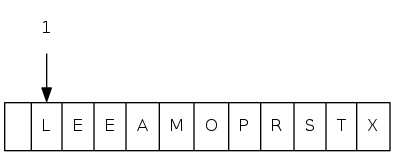
exch(4), then sink(1)

heapsort demo

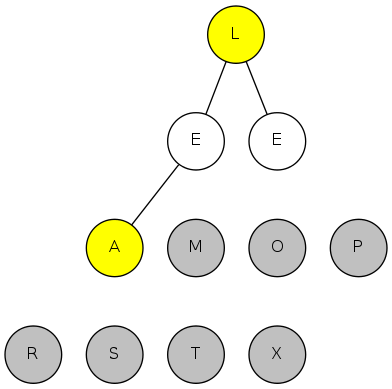
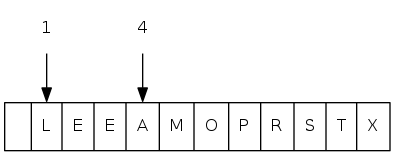
exch(4), then sink(1)

heapsort demo

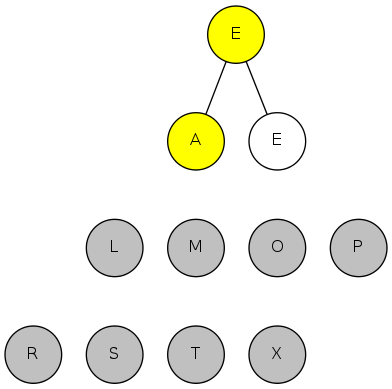
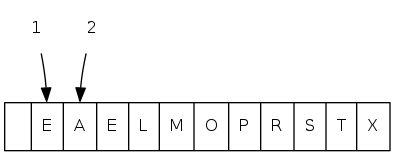
exch(3), then sink(1)

heapsort demo

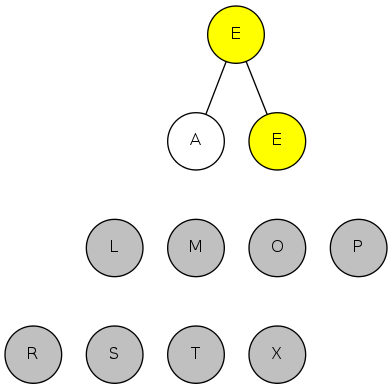
exch(3), then sink(1)

heapsort demo

exch(2), then sink(1)

heapsort demo

exch(2), then sink(1)

heapsort demo

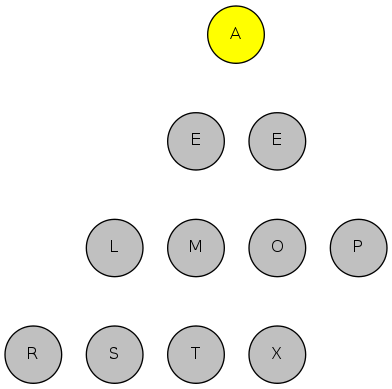
exch(1), then sink(1)

heapsort demo

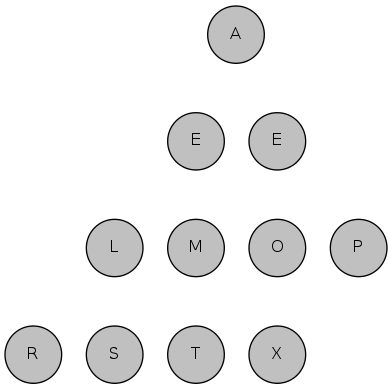
done sorting!

heapsort: heap construction

Heap construction (first pass):

Build heap using bottom-up method

for(int k = N/2; k >= 1; k--)
    sink(a, k, N);

Sortdown (second pass):

Remove the maximum, one at a time
Leave in array, instead of nulling out

while(N > 1) {
    exch(a, 1, N--);
    sink(a, 1, N);
}

heapsort: java implementation

public class Heap {
    public static void sort(Comparable[] a) {
        int N = a.length;
        for(int k = N/2; k >= 1; k--) sink(a, k, N);
        while(N > 1) {
            exch(a, 1, N);
            sink(a, 1, --N);
        }
    }

    private static void sink(Comparable[] a, int k, int N) {
        /* as before, but make static and pass arguments */
    }

    private static boolean less(Comparable[] a, int i, int j) {
        /* as before, but convert from 1-based indexing to 0-base */
    }

    private static void exch(Object[] a, int i, int j) {
        /* as before, but convert from 1-based indexing to 0-base */
    }
}

heapsort: trace

 N k   0  1  2  3  4  5  6  7  8  9 10 11
          S  O  R  T  E  X  A  M  P  L  E     initial values
11 5      .  .  .  .  L  .  .  .  .  E  E
11 4      .  .  .  T  .  .  .  M  P  .  .
11 3      .  .  X  .  .  R  A  .  .  .  .
11 2      .  T  .  P  L  .  .  M  O  .  .
11 1      X  T  S  .  .  R  A  .  .  .  .
          X  T  S  P  L  R  A  M  O  E  E     heap-ordered
10 1      T  P  S  O  L  .  .  M  E  .  X
 9 1      S  P  R  .  .  E  A  .  .  T  .
 8 1      R  P  E  .  .  E  A  .  S  .  .
 7 1      P  O  E  M  L  .  .  R  .  .  .
 6 1      O  M  E  A  L  .  P  .  .  .  .
 5 1      M  L  .  A  .  O  .  .  .  .  .
 4 1      L  E  E  A  M  .  .  .  .  .  .
 3 1      E  A  E  L  .  .  .  .  .  .  .
 2 1      E  A  E  .  .  .  .  .  .  .  .
 1 1      A  E  .  .  .  .  .  .  .  .  .
          A  E  E  L  M  O  P  R  S  T  X     sorted result

heapsort: animation

Black values are sorted

Gray values are unsorted

Red triangle marks algorithm position

[ Sorting Algorithm Animations: Heap Sort ]

heapsort: mathematical analysis

Proposition: Heap construction uses $\leq 2N$ compares and $\leq N$ exchanges

Pf sketch (assume $N = 2^{h+1}-1$):

\[\begin{array}{rcl} h + 2(h-1) + 4(h-2) + 8(h-3) + \ldots + 2^h(0) & \leq & 2^{h+1}-1 \\ & = & N \end{array}\]

note: left side of $\leq$ is a tricky sum (see Discrete Math)

heapsort: mathematical analysis

Proposition: Heapsort uses $\leq 2N \lg N$ compares and exchanges, though algorithm can be improved to $\texttilde 1 N \lg N$ (but no such variant is known to be practical)

Significance: In-place sorting algorithm with $N \log N$ worst-case

Mergesort: no, linear extra space (in-place merge possible, not practical)
Quicksort: no, quadratic time in worst case ($N \log N$ worst-case quicksort possible, but not practical)
Heapsort: yes!

heapsort: mathematical analysis

Proposition: Heapsort uses $\leq 2N \lg N$ compares and exchanges, though algorithm can be improved to $\texttilde 1 N \lg N$ (but no such variant is known to be practical)

Bottom line: Heapsort is optimal for both time and space, but...

Inner loop longer than quicksort's
Makes poor use of cache (can be improved using advanced caching tricks)
Not stable

Introsort

Goal: as fast as quicksort in practice; $N \log N$ worst case, in place

Introsort

Run quicksort
Cutoff to heapsort if stack depth exceeds $2 \lg N$
Cutoff to insertion sort for $N = 16$

In the wild: C++ STL, Microsoft .NET Framework

sorting algorithms: summary

	inplace?	stable?	best	avg	worst	remarks
selection	X		$\onehalf N^2$	$\onehalf N^2$	$\onehalf N^2$	$N$ exchanges
insertion	X	X	$N$	$\onequarter N^2$	$\onehalf N^2$	use for small $N$ or partially ordered
shell	X		$N \log_3 N$	?	$c N^a$	tight code; subquadratic
merge		X	$\onehalf N \lg N$	$N \lg N$	$N \lg N$	$N \log N$ guarantee; stable
timsort		X	$N$	$N \lg N$	$N \lg N$	improves mergesort when preexisting order
quick	X		$N \lg N$	$2 N \ln N$	$\onehalf N^2$	$N \log N$ probabilistic guarantee; fastest in practice
3-way qs	X		$N$	$2 N \ln N$	$\onehalf N^2$	improves quicksort when duplicate keys
heap	X		$N$	$2 N \lg N$	$2 N \lg N$	$N \log N$ guarantee; in-place
?	X	X	$N$	$N \lg N$	$N \lg N$	holy grail of sorting

implementation	`insert`	`delMax`	`max`
unordered array	\(1\)	\(N\)	\(N\)
ordered array	\(N\)	\(1\)	\(1\)
goal for today	\(\log N\)	\(\log N\)	\(\log N\)

implementation	`insert`	`delMax`	`max`
unordered array	\(1\)	\(N\)	\(N\)
ordered array	\(N\)	\(1\)	\(1\)
binary heap	\(\log N\)	\(\log N\)	\(1\)

implementation	`insert`	`delMax`	`max`
unordered array	\(1\)	\(N\)	\(N\)
ordered array	\(N\)	\(1\)	\(1\)
binary heap	\(\log N\)	\(\log N\)	\(1\)
\(d\)-ary heap	\(\log_d N\)	\(d \log_d N\)	\(1\)
Fibonacci	\(1\)	\(\log N^*\)	\(1\)
Brodal queue	\(1\)	\(\log N\)	\(1\)
impossible	\(1\)	\(1\)	\(1\)

	inplace?	stable?	best	avg	worst	remarks
selection	X		\(\onehalf N^2\)	\(\onehalf N^2\)	\(\onehalf N^2\)	\(N\) exchanges
insertion	X	X	\(N\)	\(\onequarter N^2\)	\(\onehalf N^2\)	use for small \(N\) or partially ordered
shell	X		\(N \log_3 N\)	?	\(c N^a\)	tight code; subquadratic
merge		X	\(\onehalf N \lg N\)	\(N \lg N\)	\(N \lg N\)	\(N \log N\) guarantee; stable
timsort		X	\(N\)	\(N \lg N\)	\(N \lg N\)	improves mergesort when preexisting order
quick	X		\(N \lg N\)	\(2 N \ln N\)	\(\onehalf N^2\)	\(N \log N\) probabilistic guarantee; fastest in practice
3-way qs	X		\(N\)	\(2 N \ln N\)	\(\onehalf N^2\)	improves quicksort when duplicate keys
heap	X		\(N\)	\(2 N \lg N\)	\(2 N \lg N\)	\(N \log N\) guarantee; in-place
?	X	X	\(N\)	\(N \lg N\)	\(N \lg N\)	holy grail of sorting