Merge Sorts
COS 265 - Data Structures & Algorithms
two classic sorting algorithms: merge sort and quicksort
Critical components in the world's computational infrastructure
- Full scientific understanding of their properties has enabled us to develop them into practical system sorts
- Quicksort honored as one of top 10 algorithms of 20th century in science and engineering.
Merge sort: this lecture
Quicksort: next lecture
Merge Sorts
merge sort
merge sort
Basic plan
- Divide array into two halves
- Recursively sort each half
- Merge two (sorted) halves
input: M E R G E S O R T E X A M P L E two halves: M E R G E S O R T E X A M P L E sort left half: E E G M O R R S < T E X A M P L E sort right half: E E G M O R R S > A E E L M P T X merge results: A E E E E G L M M O P R R S T X merged: A E E E E G L M M O P R R S T X


merge sort demo
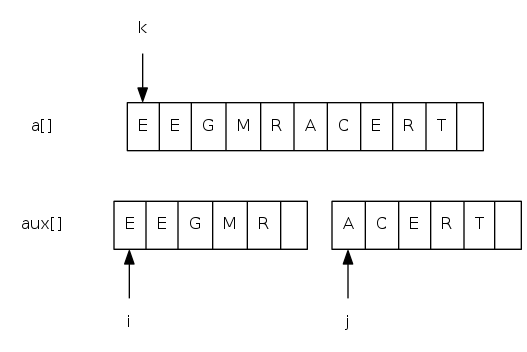
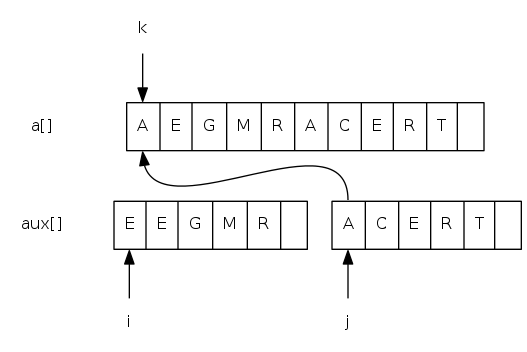
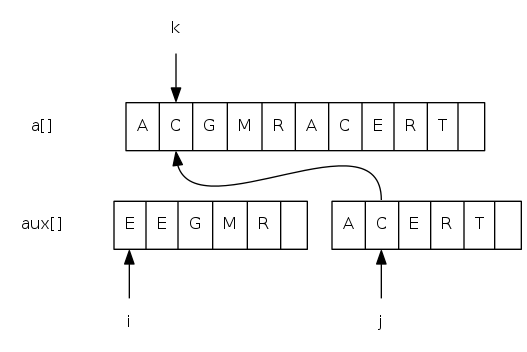
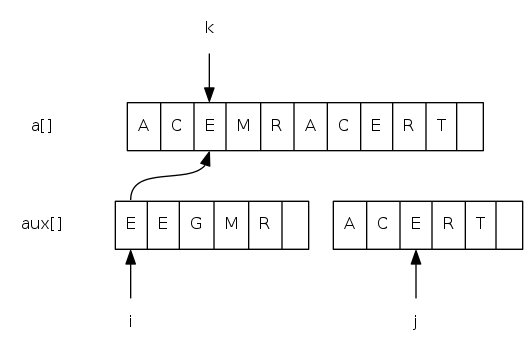
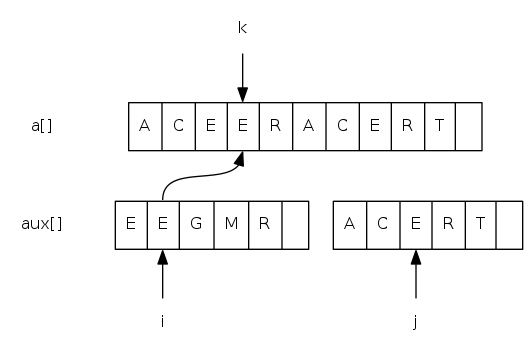
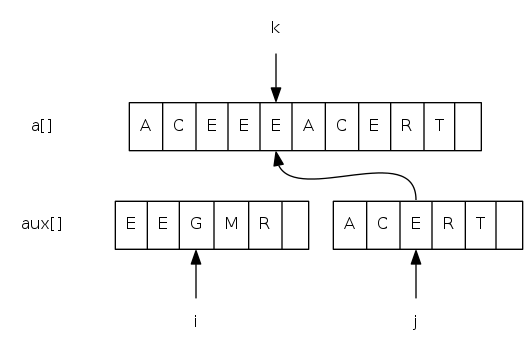
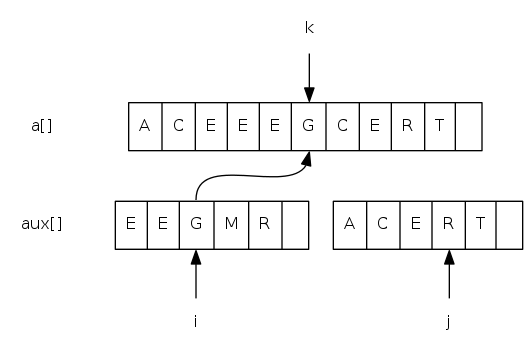
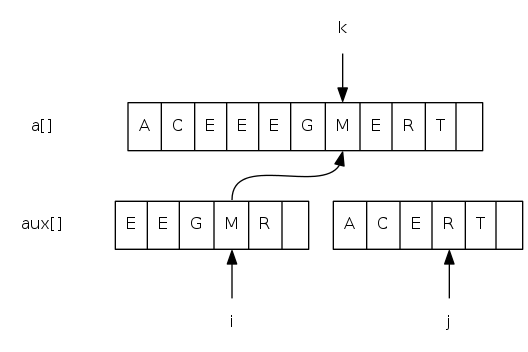
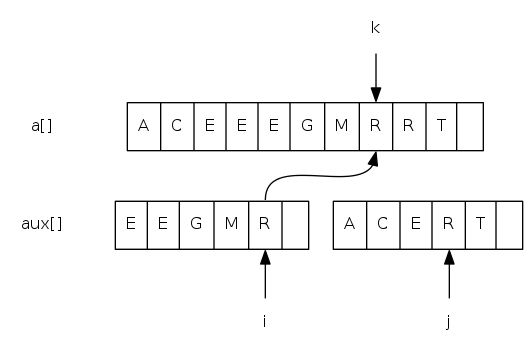
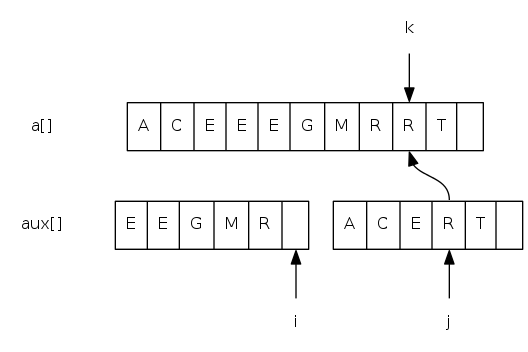
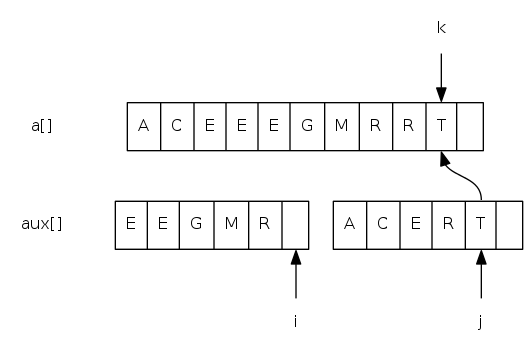
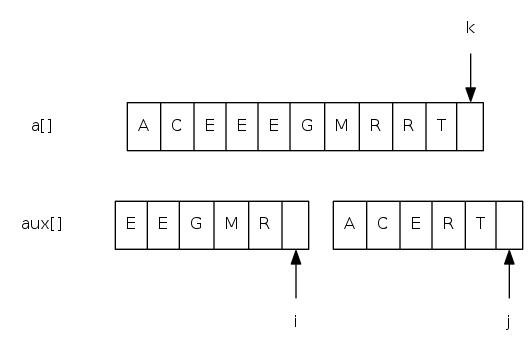
Goal: given two sorted subarrays a[lo] to a[mid] and a[mid+1] to a[hi], replace with sorted subarray a[lo] to a[hi].

merge sort demo
merge sort demo
merge sort demo
merge sort demo
merge sort demo
merge sort demo
merge sort demo
merge sort demo
merge sort demo
merge sort demo
merge sort demo
merge sort demo
merge sort demo

merging: java implementation
private static void merge(Comparable[] a, Comparable[] aux,
int lo, int mid, int hi) {
for(int k = lo; k <= hi; k++) aux[k] = a[k]; // copy
int i = lo, j = mid + 1;
for(int k = lo; k <= hi; k++) {
if(i > mid) a[k] = aux[j++]; // merge
else if(j > hi) a[k] = aux[i++];
else if(less(aux[j], aux[i])) a[k] = aux[j++];
else a[k] = aux[i++];
}
}
// lo i mid j hi
// | | | | |
aux[] = { A G L O R|H I M S T }
a[] = { A G H I L M ? ? ? ? }
// |
// k
merging: java implementation
public class Merge {
private static void merge(/*...*/) { /* as before */ }
private static void sort(Comparable[] a, Comparable[] aux,
int lo, int hi) {
if(hi <= lo) return;
int mid = lo + (hi - lo) / 2;
sort(a, aux, lo, mid);
sort(a, aux, mid+1, hi);
merge(a, aux, lo, mid, hi);
}
public static void sort(Comparable[] a) {
Comparable[] aux = new Comparable[a.length];
sort(a, aux, 0, a.length - 1);
}
}
Merge sort: trace
0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5
lo hi M E R G E S O R T E X A M P L E
merge(a, aux, 0, 0, 1) E M . . . . . . . . . . . . . .
merge(a, aux, 2, 2, 3) . . G R . . . . . . . . . . . .
merge(a, aux, 0, 1, 3) E G M R . . . . . . . . . . . .
merge(a, aux, 4, 4, 5) . . . . E S . . . . . . . . . .
merge(a, aux, 6, 6, 7) . . . . . . O R . . . . . . . .
merge(a, aux, 4, 5, 7) . . . . E O R S . . . . . . . .
merge(a, aux, 0, 3, 7) E E G M O R R S . . . . . . . .
merge(a, aux, 8, 8, 9) . . . . . . . . E T . . . . . .
merge(a, aux, 10, 10, 11) . . . . . . . . . . A X . . . .
merge(a, aux, 8, 9, 11) . . . . . . . . A E T X . . . .
merge(a, aux, 12, 12, 13) . . . . . . . . . . . . M P . .
merge(a, aux, 14, 14, 15) . . . . . . . . . . . . . . E L
merge(a, aux, 12, 13, 15) . . . . . . . . . . . . E M L P
merge(a, aux, 8, 11, 15) . . . . . . . . A E E L M P T X
merge(a, aux, 0, 7, 15) A E E E E G L M M O P R R S T X
merge sort: animation



Black values are sorted
Gray values are unsorted
Red triangle marks algorithm position
Dark gray values denote the current interval
merge sort: empirical analysis
Running time estimates of insertion vs. merge sort:
- Laptop executes \(10^8\) compares/second
- Supercomputer executes \(10^{12}\) compares/second
| computer | IS 1k | IS 1m | IS 1b | MS 1k | MS 1m | MS 1b |
|---|---|---|---|---|---|---|
| home | instant | 2.8hrs | 317yrs | instant | 1sec | 18min |
| super | instant | 1sec | 1wk | instant | instant | instant |
Bottom line: Good algorithms are better than supercomputers.
merge sort: number of compares
Proposition: Merge sort uses \(\leq N \lg N\) compares to sort an array of length \(N\).
Pf sketch: The number of compares \(C(N)\) to merge sort an array of length \(N\) satisfies the recurrence
\[ C(N) \leq \underbrace{C(\lceil N/2 \rceil)}_{\text{left half}} + \underbrace{C(\lfloor N/2 \rfloor)}_{\text{right half}} + \underbrace{N}_{\text{merge}} \text{ for } N > 1, \text{ with } C(1) = 0 \]
We solve the recurrence when \(N\) is a power of 2 (result holds for all \(N\), analysis cleaner in this case):
\[D(N) = 2 D(N/2) + N, \text{ for } N > 1, \text{ with } D(1) = 0\]
divide-and-conquer recurrence
Proposition: If \(D(N)\) satisfies \(D(N) = 2 D(N/2) + N\) for \(N > 1\), with \(D(1) = 0\), then \(D(N) = N \lg N\)
Pf by picture (assuming \(N\) is a power of 2):
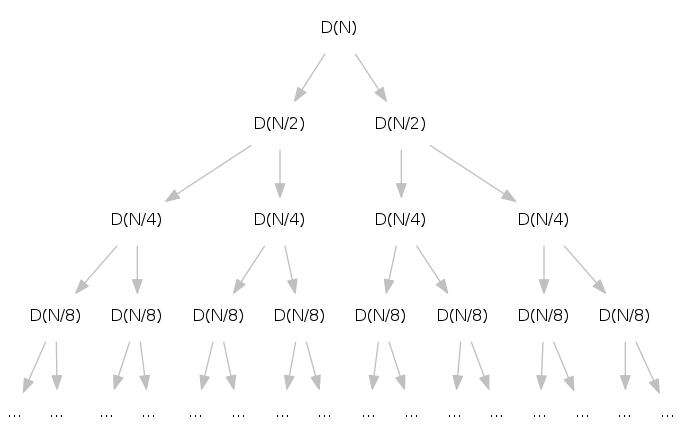
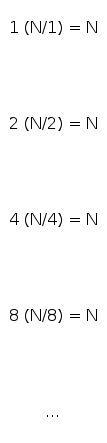
Height of binary tree: \(\lg N\)
Recurrence: \(T(N) = N \lg N\)
divide-and-conquer recurrence
Proposition: If \(D(N)\) satisfies \(D(N) = 2 D(N/2) + N\) for \(N > 1\), with \(D(1) = 0\), then \(D(N) = N \lg N\)
Pf by induction (assuming \(N\) is a power of 2):
- Base case: \(N = 1\)
- Inductive hypothesis: \(D(N) = N \lg N\)
- Goal: show that \(D(2N) = (2N) \lg (2N)\)
\[ \begin{array}{rcll} D(2N) & = & 2 D(N) + 2N & \text{given} \\ & = & 2N \lg N + 2N & \text{inductive hypothesis} \\ & = & 2N (\lg (2N) - 1) + 2N & \text{algebra} \\ & = & 2N \lg (2N) & \text{QED} \\ \end{array} \]
merge sort: number of array accesses
Proposition: Merge sort uses \(\leq 6 N \lg N\) array accesses to sort an array of length \(N\)
Pf sketch: The number of array accesses \(A(N)\) satisfies the recurrence:
\[A(N) \leq A(\lceil N / 2 \rceil) + A(\lfloor N / 2 \rfloor) + 6N \text{ for } N > 1, \text{ with } A(1) = 0\]
Key point: any algorithm with the following structure takes \(N \log N\) time
public static void linearithmic(int N) {
if(N == 0) return;
linearithmic(N/2); // solve two problems
linearithmic(N/2); // of half the size
linear(N); // do a linear amount of work
}
Notable examples: FFT, hidden-line removal, Kendall-tau distance, ...
merge sort analysis: memory
Proposition: Merge sort uses extra space proportional to \(N\)
Pf: The array aux[] needs to be of length \(N\) for the last merge
two sorted subarrays
A C D G H I M N U V B E F J O P Q R S T
A B C D E F G H I J M N O P Q R S T U V
merged result
Def: A sorting algorithm is in-place if it uses \(\leq c \log N\) extra memory
Ex: Insertion sort, selection sort, shellsort
Challenge 1 (not hard): Use aux[] array of length \(\texttilde \frac{1}{2} N\)
instead of \(N\)
Challenge 2 (very hard): In-place merge [Kronrod 1969]
merge sort: practical improvements
Use insertion sort for small subarrays
- Merge sort has too much overhead for tiny subarrays
- Cutoff to insertion sort for \(\leq\) 10 items
private static void sort(Comparable[] a, Comparable[] aux,
int lo, int hi) {
if(hi <= lo + CUTOFF - 1) {
Insertion.sort(a, lo, hi);
return;
}
int mid = lo + (hi - lo) / 2;
sort(a, aux, lo, mid);
sort(a, aux, mid+1, hi);
merge(a, aux, lo, mid, hi);
}
merge sort with cutoff in insertion sort
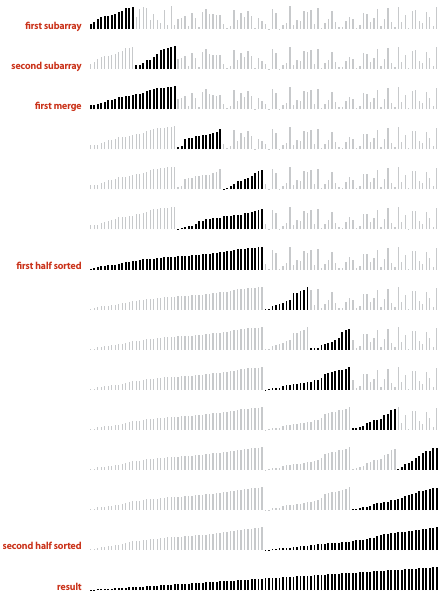
merge sort: practical improvements
Stop (no need to merge) if already sorted
- Is largest item in first half \(\leq\) smallest item in second half?
- Helps for partially-ordered arrays
A B C D E F G H I J M N O P Q R S T U V
^ > ^
private static void sort(Comparable[] a, Comparable[] aux,
int lo, int hi) {
if(hi <= lo) return;
int mid = lo + (hi-lo) / 2;
sort(a, aux, lo, mid);
sort(a, aux, mid+1, hi);
if(!less(a[mid+1], a[mid])) return;
merge(a, aux, lo, mid, hi);
}
merge sort: practical improvements
Eliminate the copy to the auxiliary array: save time (but not space) by switching the role of the input and auxiliary array in each recursive call.
private static void sort(Comparable[] a, Comparable[] aux,
int lo, int mid, int hi) {
// don't need to copy from a[] to aux[]
// if we merge from a[] to aux[]
int i = lo, j = mid + 1;
for(int k = lo; k <= hi; k++) {
if(i > mid) aux[k] = a[j++];
else if(j > hi) aux[k] = a[i++];
else if(less(aux[j], aux[i])) aux[k] = a[j++];
else aux[k] = a[i++];
}
}
private static void sort(Comparable[] a, Comparable[] aux,
int lo, int hi) {
// note: assuming aux[] is initialized to a[] once, before
// recursive calls!
if(hi <= lo) return;
int mid = lo + (hi-lo) / 2;
sort(aux, a, lo, mid); // switch roles of
sort(aux, a, mid+1, hi); // aux[] and a[]
merge(a, aux, lo, mid, hi);
}
java 6 system sort
Basic algorithm for sorting objects = merge sort
- Cutoff to insertion sort = 7
- Stop-if-already-sorted test
- Eliminate-the-copy-to-the-auxiliary-array trick
Array.sort(a)
merge sort
bottom-up merge sort
bottom-up merge sort
Basic plan
- Pass through array, merging subarrays of size 1
- Repeat for subarrays of size 2, 4, 8, ...
0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5
lo hi M E R G E S O R T E X A M P L E
sz=1
merge(a, aux, 0, 0, 1) E M . . . . . . . . . . . . . .
merge(a, aux, 2, 2, 3) . . G R . . . . . . . . . . . .
merge(a, aux, 4, 4, 5) . . . . E S . . . . . . . . . .
merge(a, aux, 6, 6, 7) . . . . . . O R . . . . . . . .
merge(a, aux, 8, 8, 9) . . . . . . . . E T . . . . . .
merge(a, aux, 10, 10, 11) . . . . . . . . . . A X . . . .
merge(a, aux, 12, 12, 13) . . . . . . . . . . . . M P . .
merge(a, aux, 14, 14, 15) . . . . . . . . . . . . . . E L
sz = 2
merge(a, aux, 0, 1, 3) E G M R . . . . . . . . . . . .
merge(a, aux, 4, 5, 7) . . . . E O R S . . . . . . . .
merge(a, aux, 8, 9, 11) . . . . . . . . A E T X . . . .
merge(a, aux, 12, 13, 15) . . . . . . . . . . . . E M L P
sz = 4
merge(a, aux, 0, 3, 7) E E G M O R R S . . . . . . . .
merge(a, aux, 8, 11, 15) . . . . . . . . A E E L M P T X
sz = 8
merge(a, aux, 0, 7, 15) A E E E E G L M M O P R R S T X
bottom-up merge sort: java implementation
public class MergeBU {
private static void merge(/*...*/) { /* as before */ }
public static void sort(Comparable[] a) {
int N = a.length;
Comparable[] ax = new Comparable[N];
for(int sz = 1; sz < N; sz = sz+sz)
for(int lo = 0; lo < N-sz; lo += sz+sz)
merge(a, aux, lo, lo+sz-1, Math.min(lo+sz+sz-1, N-1));
}
}
Bottom line: simple and non-recursive version of merge sort (but about 10% slower than recursive, top-down merge sort on typical systems)
merge sort: visualizations
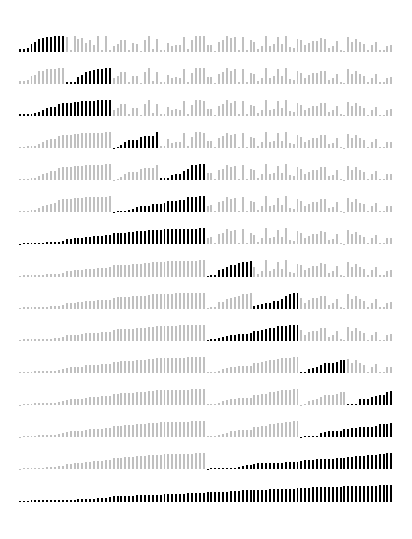
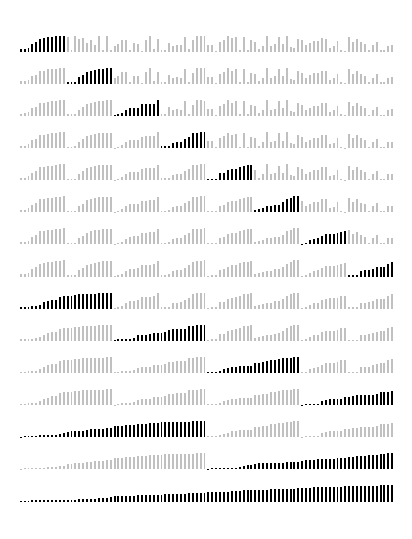
natural merge sort
Idea: Exploit pre-existing order by identifying naturally-occurring runs
input: 1 5 10 16 3 4 23 9 13 2 7 8 12 14 first run: 1 5 10 16 . . . . . . . . . . second run: . . . . 3 4 23 . . . . . . . merge two runs: 1 3 4 5 10 16 23 . . . . . . .
Tradeoff: Fewer passes vs. extra compares per pass to identify runs
timsort
- Natural merge sort
- Use binary insertion sort to make initial runs (if needed)
- A few more clever optimizations
Intro ----- This describes an adaptive, stable, natural mergesort, modestly called timsort (hey, I earned it <wink>). It has supernatural performance on many kinds of partially ordered arrays (less than lg(N!) comparisons needed, and as few as N-1), yet as fast as Python's previous highly tuned samplesort hybrid on random arrays. In a nutshell, the main routine marches over the array once, left to right, alternately identifying the next run, then merging it into the previous runs "intelligently". Everything else is complication for speed, and some hard-won measure of memory efficiency. ...
Consequence: Linear time on many arrays with pre-existing order
Now widely used: Python, Java 7, GNU Octave, Android, ...
the zen of python

merge sort
sorting complexity
complexity of sorting
Computational complexity: Framework to study efficiency of algorithms for solving a particular problem \(X\).
- Model of computation: Allowable operations
- Cost model: Operation count(s)
- Upper bound: Cost guarantee provided by some algorithm for \(X\)
- Lower bound: Proven limit on cost guarantee of all algorithms for \(X\)
- Optimal algorithm: Algorithm with best possible cost guarantee for \(X\) (lower bound \(\texttilde\) upper bound)
complexity of sorting
Example: sorting
- Model of computation: decision tree (can access information only through compares, e.g., Java comparable framework)
- Cost model: number of compares
- Upper bound: \(\texttilde N \lg N\) from merge sort
- Lower bound:
- Optimal algorithm:
decision tree (for 3 distinct keys a, b, c)
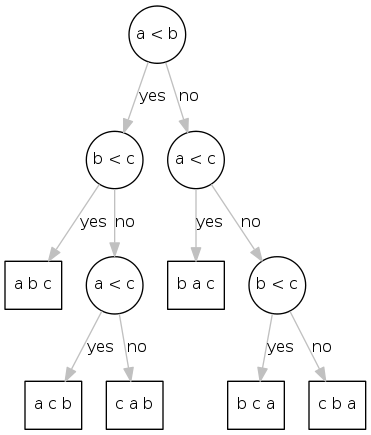 |
code between compares (e.g., sequence of exchanges) height of tree = worst-case number of compares each leaf corresponds to one (and only one) ordering; (at least) one leaf for each possible ordering |
compare-based lower bound for sorting
Proposition: Any compare-based sorting algorithm must use at least \(\lg(N!) \texttilde N \lg N\) compares in the worst-case
Pf:
- Assume array consists of \(N\) distinct values \(a_1\) through \(a_N\)
- Worst case dictated by height \(h\) of decision tree
- Binary tree of height \(h\) has at most \(2^h\) leaves
- \(N!\) different orderings → at least \(N!\) leaves
\[2^h \geq \text{num of leaves} \geq N!\] \[ \Rightarrow h \geq \lg(N!) \texttilde N \lg N\]
complexity of sorting
- Model of computation: Allowable operations
- Cost model: Operation count(s)
- Upper bound: Cost guarantee provided by some algorithm for \(X\)
- Lower bound: Proven limit on cost guarantee of all algorithms for \(X\)
- Optimal algorithm: Algorithm with best possible cost guarantee for \(X\) (lower bound \(\texttilde\) upper bound)
complexity of sorting
Example: sorting
- Model of computation: decision tree (can access information only through compares, e.g., Java comparable framework)
- Cost model: number of compares
- Upper bound: \(\texttilde N \lg N\) from merge sort
- Lower bound: \(\texttilde N \lg N\)
- Optimal algorithm: merge sort
First goal of algorithm design: optimal algorithms
complexity results in context
Compares? Merge sort is optimal with respect to number of compares
Space? Merge sort is not optimal with respect to space usage
Lessons: Use theory as a guide
Ex: Design sorting algorithm that guarantees \(\frac{1}{2} N \lg N\) compares
Ex: Design sorting algorithm that is both time- and space-optimal
complexity results in context
Lower bound may not hold if the algorithm can take advantage of:
-
The initial order of the input
Ex: insert sort requires only a linear number of compares on partially-sorted arrays -
The distribution of key values
Ex: 3-way quicksort requires only a linear number of compares on arrays with a constant number of distinct keys (stay tuned) -
The representation of the keys
Ex: radix sort requires no key compares—it accesses the data via character/digit compares
Merge sort
comparators
sort countries
Sort countries by gold medals
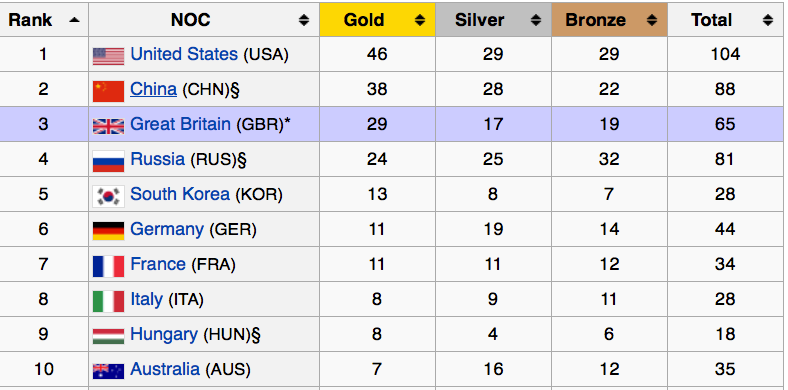
sort countries
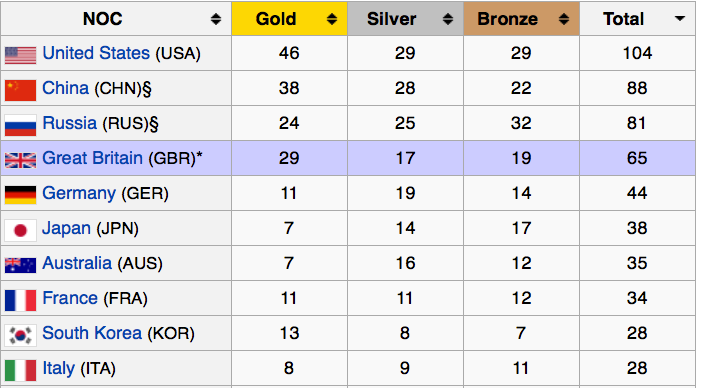
Sort countries by all medals
sort music library
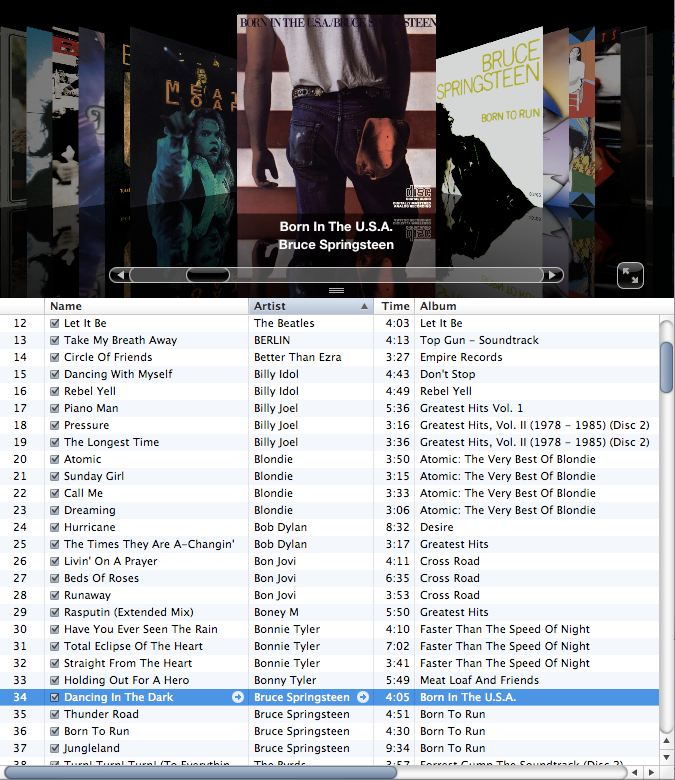
Sort music library by artist
sort music library
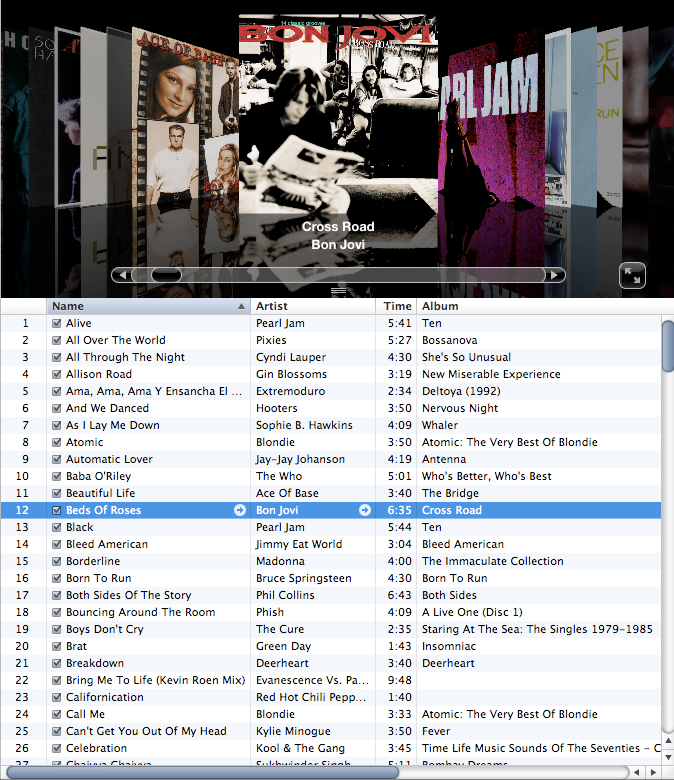
Sort music library by song name
Comparable interface: review
Comparable interface: sort using a type's natural order
public class Date implements Comparable<Date> {
private final int month, day, year;
public Date(int m, int d, int y) {
month = m;
day = d;
year = y;
}
public int compareTo(Date that) {
if(this.year < that.year ) return -1;
if(this.year > that.year ) return +1;
if(this.month < that.month) return -1;
if(this.month > that.month) return +1;
if(this.day < that.day ) return -1;
if(this.day > that.day ) return +1;
return 0;
}
}
Comparator interface
Comparator interface: sort using an alternate order
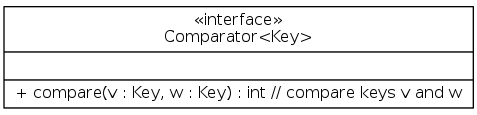
Required property: Must be a total order
| string order | example |
|---|---|
| natural order | Now is the time |
| case insensitive | is Now the time |
| Spanish language | café cafetero cuarto churro nube ñoño |
| British phone book | McKinley Mackintosh |
Spanish language: pre-1994 order for digraphs ch and ll and rr
Comparator interface: system sort
To use with Java system sort:
- Create
Comparatorobject - Pass as second argument to
Arrays.sort()
String[] a = {"foo","bar","baz"}
// sort using natural order
Arrays.sort(a);
// sort using alternate order defined by Comparator<String> object
Arrays.sort(a, String.CASE_INSENSITIVE_ORDER);
Arrays.sort(a, Collator.getInstance(new Locale("es")));
Arrays.sort(a, new BritishPhoneBookOrder());
Bottom line: Decouples the definition of the data type from the definition of what it means to compare two objects of that type.
Comparator interface: using with our sorting libraries
To support comparators in our sort implementations:
- Use
Objectinstead ofComparable - Pass
Comparatortosort()andless()and use it inless()
// insertion sort using a Comparator
public static void sort(Object[] a, Comparator comparator) {
int N = a.length;
for(int i = 0; i < N; i++)
for(int j = i; j > 0 && less(comparator, a[j], a[j-1]); j--)
exch(a, j, j-1);
}
private static boolean less(Comparator c, Object v, Object w) {
return c.compare(v, w) < 0;
}
private static void exch(Object[] a, int i, int j) {
Object swap = a[i]; a[i] = a[j]; a[j] = swap;
}
Comparator interface: implementing
To implement a comparator:
- Define a (nested) class that implements the
Comparatorinterface - Implement the
compare()method
public class Student {
private final String name;
private final int section;
public static class ByName implements Comparator<Student> {
public int compare(Student v, Student w) {
return v.name.compareTo(w.name);
}
}
public static class BySection implements Comparator<Student> {
public int compare(Student v, Student w) {
// this trick works here since no danger of overflow
return v.section - w.section;
}
}
}
Comparator interface: implementing
Arrays.sort(a, new Student.ByName());
| Andrews | 3 | A | 664-480-0023 | 97 Little |
| Battle | 4 | C | 874-088-1212 | 121 Whitman |
| Chen | 3 | A | 991-878-4944 | 308 Blair |
| Fox | 3 | A | 884-232-5341 | 11 Dickinson |
| Furia | 1 | A | 766-093-9873 | 101 Brown |
| Gazsi | 4 | B | 766-093-9873 | 101 Brown |
| Kanaga | 3 | B | 898-122-9643 | 22 Brown |
| Rohde | 2 | A | 232-343-5555 | 343 Forbes |
Comparator interface: implementing
Arrays.sort(a, new Student.BySection());
| Furia | 1 | A | 766-093-9873 | 101 Brown |
| Rohde | 2 | A | 232-343-5555 | 343 Forbes |
| Andrews | 3 | A | 664-480-0023 | 97 Little |
| Chen | 3 | A | 991-878-4944 | 308 Blair |
| Fox | 3 | A | 884-232-5341 | 11 Dickinson |
| Kanaga | 3 | B | 898-122-9643 | 22 Brown |
| Battle | 4 | C | 874-088-1212 | 121 Whitman |
| Gazsi | 4 | B | 766-093-9873 | 101 Brown |
Merge sort
stability
Stability
A typical application: First, sort by name; then, sort by section
Selection.sort(a, new Student.ByName()); // <=== Selection.sort(a, new Student.BySection());
| Andrews | 3 | A | 664-480-0023 | 97 Little |
| Battle | 4 | C | 874-088-1212 | 121 Whitman |
| Chen | 3 | A | 991-878-4944 | 308 Blair |
| Fox | 3 | A | 884-232-5341 | 11 Dickinson |
| Furia | 1 | A | 766-093-9873 | 101 Brown |
| Gazsi | 4 | B | 766-093-9873 | 101 Brown |
| Kanaga | 3 | B | 898-122-9643 | 22 Brown |
| Rohde | 2 | A | 232-343-5555 | 343 Forbes |
Stability
A typical application: First, sort by name; then, sort by section
Selection.sort(a, new Student.ByName()); Selection.sort(a, new Student.BySection()); // <===
| Furia | 1 | A | 766-093-9873 | 101 Brown |
| Rohde | 2 | A | 232-343-5555 | 343 Forbes |
| Chen | 3 | A | 991-878-4944 | 308 Blair |
| Fox | 3 | A | 884-232-5341 | 11 Dickinson |
| Andrews | 3 | A | 664-480-0023 | 97 Little |
| Kanaga | 3 | B | 898-122-9643 | 22 Brown |
| Gazsi | 4 | B | 766-093-9873 | 101 Brown |
| Battle | 4 | C | 874-088-1212 | 121 Whitman |
Stability
A typical application: First, sort by name; then, sort by section
Selection.sort(a, new Student.ByName()); Selection.sort(a, new Student.BySection()); // <===
| Furia | 1 | A | 766-093-9873 | 101 Brown |
| Rohde | 2 | A | 232-343-5555 | 343 Forbes |
| Chen | 3 | A | 991-878-4944 | 308 Blair |
| Fox | 3 | A | 884-232-5341 | 11 Dickinson |
| Andrews | 3 | A | 664-480-0023 | 97 Little |
| Kanaga | 3 | B | 898-122-9643 | 22 Brown |
| Gazsi | 4 | B | 766-093-9873 | 101 Brown |
| Battle | 4 | C | 874-088-1212 | 121 Whitman |
Argh! Students in section 3 no longer sorted by name!
A stable sort preserves the relative order of items with equal keys
stability
Q. Which sorts are stable?
A. Need to check algorithm (and implementation)
| Chicago | 09:00:00 | Chicago | 09:25:52 | Chicago | 09:00:00 | ||
| Phoenix | 09:00:03 | Chicago | 09:03:13 | Chicago | 09:00:59 | ||
| Houston | 09:00:13 | Chicago | 09:21:05 | Chicago | 09:03:13 | ||
| Chicago | 09:00:59 | Chicago | 09:19:46 | Chicago | 09:19:32 | ||
| Houston | 09:01:10 | Chicago | 09:19:32 | Chicago | 09:19:46 | ||
| Chicago | 09:03:13 | Chicago | 09:00:00 | Chicago | 09:21:05 | ||
| Seattle | 09:10:11 | Chicago | 09:35:21 | Chicago | 09:25:52 | ||
| Seattle | 09:10:25 | Chicago | 09:00:59 | Chicago | 09:35:21 | ||
| Phoenix | 09:14:25 | Houston | 09:01:10 | Houston | 09:00:13 | ||
| Chicago | 09:19:32 | Houston | 09:00:13 | Houston | 09:01:10 | ||
| Chicago | 09:19:46 | Phoenix | 09:37:44 | Phoenix | 09:00:03 | ||
| Chicago | 09:21:05 | Phoenix | 09:00:03 | Phoenix | 09:14:25 | ||
| Seattle | 09:22:43 | Phoenix | 09:14:25 | Phoenix | 09:37:44 | ||
| Seattle | 09:22:54 | Seattle | 09:10:25 | Seattle | 09:10:11 | ||
| Chicago | 09:25:52 | Seattle | 09:36:14 | Seattle | 09:10:25 | ||
| Chicago | 09:35:21 | Seattle | 09:22:43 | Seattle | 09:22:43 | ||
| Seattle | 09:36:14 | Seattle | 09:10:11 | Seattle | 09:22:54 | ||
| Phoenix | 09:37:44 | Seattle | 09:22:54 | Seattle | 09:36:14 | ||
| sorted | sorted | not stable | sorted | stable |
stability: insertion sort
Proposition: Insertion sort is stable
public class Insertion {
public static void sort(Comparable[] a) {
int N = a.length;
for(int i = 0; i < N; i++)
for(int j = i; j > 0 && less(a[j], a[j-1]); j--)
exch(a, j, j-1);
}
}
i j 0 1 2 3 4
B1 A1 A2 A3 B2
0 0 B1 . . . .
1 0 A1 B1 . . .
2 1 . A2 B1 . .
3 2 . . A3 B1 .
4 4 . . . . B2
A1 A2 A3 B1 B2
Pf: Equal items never move past each other
stability: Selection sort
Proposition: Selection sort is not stable
public class Selection {
public static void sort(Comparable[] a) {
int N = a.length;
for(int i = 0; i < N; i++) {
int min = i;
for(int j = i+1; j < N; j++)
if(less(a[j], a[min])) min = j;
exch(a, i, min);
}
}
}
i min 0 1 2
B1 B2 A
0 2 A . B1
1 1 . B2 .
2 2 . . B1
A B2 B1
Pf by counterexample: Long-distance exchange can move one equal item past another one
stability: shellsort
Proposition: Shellsort is not stable
public class Shell {
public static void sort(Comparable[] a) {
int N = a.length;
int h = 1;
while(h < N/3) h = 3 * h + 1;
while(h >= 1) {
for(int i = h; i < N; i++) {
for(int j = i; j > h && less(a[j], a[j-h]); j -= h)
exch(a, j, j-h);
}
h = h / 3;
}
}
}
h 0 1 2 3 4
B1 B2 B3 B4 A1
4 A1 . . . B1
1 . . . . .
A1 B2 B3 B4 B1
Pf by counterexample: Long-distance exchanges
stability: mergesort
Proposition: Mergesort is stable
public class Merge {
private static void merge(/*...*/) { /* as before */ }
private static void sort(Comparable[] a, Comparable[] aux,
int lo, int hi) {
if(hi <= lo) return;
int mid = lo + (hi - lo) / 2;
sort(a, aux, lo, mid);
sort(a, aux, mid+1, hi);
merge(a, aux, lo, mid, hi);
}
public static void sort(Comparable[] a) { /* as before */ }
}
Pf: Suffices to verify that merge operation is stable
stability: mergesort
Proposition: Mergesort is stable
public static void merge( /*...*/ ) {
for(int k = lo; k <= hi; k++) aux[k] = a[k];
int i = lo, j = mid+1;
for(int k = lo; k <= hi; k++) {
if (i > mid) a[k] = aux[j++];
else if(j > hi) a[k] = aux[i++];
else if(less(aux[j], aux[i])) a[k] = aux[j++];
else a[k] = aux[i++];
}
}
0 1 2 3 4 5 6 7 8 9 10 A1 A2 A3 B1 D1 A4 A5 C1 E1 F1 G1 A1 A2 A3 A4 A5 B1 C1 D1 E1 F1 G1
Pf: Takes from left subarray if equal keys
sorting summary
| inplace? | stable? | best | avg | worst | remarks | |
|---|---|---|---|---|---|---|
| selection | ✔ | \(\onehalf N^2\) | \(\onehalf N^2\) | \(\onehalf N^2\) | \(N\) exchanges | |
| insertion | ✔ | ✔ | \(N\) | \(\onequarter N^2\) | \(\onehalf N^2\) | use for small \(N\) or partially ordered |
| shellsort | ✔ | \(N \log_3 N\) | ? | \(c N^a\) | tight code; subquadratic (\(a=3/2\)) | |
| merge | ✔ | \(\onehalf N \lg N\) | \(N \lg N\) | \(N \lg N\) | \(N \log N\) guaranteed; stable | |
| timsort | ✔ | \(N\) | \(N \lg N\) | \(N \lg N\) | improves merge sort when preexisting order | |
| ? | ✔ | ✔ | \(N\) | \(N \lg N \) | \(N \lg N\) | holy sorting grail |
