Bags, Queues, and Stacks
COS 265 - Data Structures & Algorithms
Bags, Queues, and Stacks
introduction
stacks and queues
Fundamental data types
- Value: collection of objects
- Operations: insert, remove, iterate, test if empty
- Intent is clear when we insert
- Which item do we remove?
stacks and queues
Stack: examine the item most recently added (LIFO)
Queue: examine the item least recently added (FIFO)

stacks and queues
Separate interface and implementation
For example: stack, queue, bag, priority queue, symbol table, union-find, ...
Benefits:
- client can't know details of implementation ⇒ client has many implementation from which to choose
- implementation can't know details of client needs ⇒ many clients can re-use the same implementation
- design: creates modular, reusable libraries
- performance: use optimized implementation where it matters
definitions
- Client
- program using operations defined in interface
- Implementation
- actual code implementing operations
- Interface
- description of data type, basic operations
Bags, Queues, and Stacks
stacks
stack api
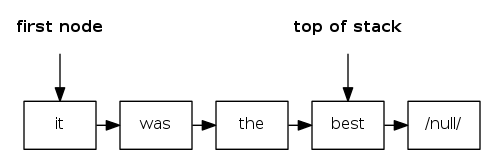
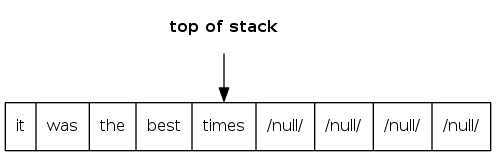
Warmup API: stack of strings data type
 |
 |
Warmup client: reverse sequence of strings from standard input
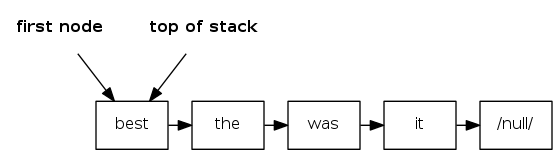
how to implement a stack with a linked list?
A. Can't be done efficiently with a singly-linked list.
B.
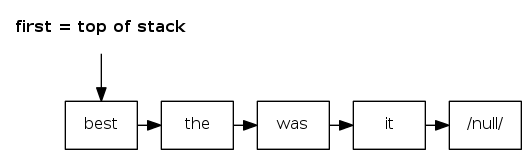
C.
stack: linked-list implementation
- Maintain pointer
firstto first node in a singly-linked list - Push new item before
first - Pop item from
first
// inner class
private class Node {
String item;
Node next;
}
stack pop: linked-list implementation
public String pop() {
String item = first.item; // save item to return
first = first.next; // delete first node
return item; // return saved item
}

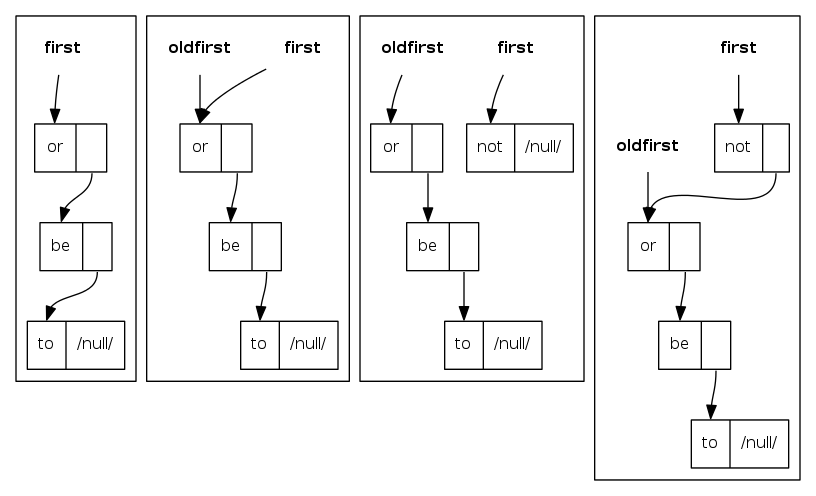
stack push: linked-list implementation
public void push(String item) {
Node oldfirst = first; // save a link to the list
first = new Node(); // create a new node for the beginning
first.item = item; // set the instance variables in
first.next = oldfirst; // the new node
}
stack: linked-list implementation in java
public class LinkedStackOfStrings {
private Node first = null;
private class Node { // private inner class
String item; // (access modifiers for instance
Node next; // variables don't matter)
}
public boolean isEmpty() {
return first == null;
}
public void push(String item) {
Node oldfirst = first;
first = new Node();
first.item = item;
first.next = oldfirst;
}
public String pop() {
String item = first.item;
first = first.next;
return item;
}
}
stack linked-list: performance
Proposition: Every operation takes constant time in the worst case
Proposition: A stack with \(N\) items uses \(\texttilde 40 N\) bytes.
private class Node {
String item;
Node next;
}
|
 |
Remark: This accounts for the memory for the stack, but not the memory for Strings themselves, which the client owns.
how to: a fixed-capacity stack with array?
A. Can't be done efficiently with an array?
B.
C.

fixed-capacity stack: array implementation
- Use array
s[]to storeNitems on stack push(): add new item ats[N]pop(): remove item froms[N-1]

Defect: Stack overflows when N exceeds capacity! (stay tuned...)
fixed-capacity stack: array implementation
public class FixedCapacityStackOfStrings {
private String[] s;
private int N = 0;
public FixedCapacityStackOfStrings(int capacity) {
s = new String[capacity]; // a cheat (stay tuned!)
}
public boolean isEmpty() {
return N == 0;
}
public void push(String item) {
s[N++] = item; // use to index into array, then increment N
}
public String pop() {
return s[--N]; // decrement N, then use to index into array
}
}
stack considerations
Overflow and underflow
- Underflow: throw exception if pop from an empty stack
- Overflow: use resizing array for array implementation (stay tuned)
Null items: we allow null items to be inserted
Loitering: holding a reference to an object when it is no longer needed
stack considerations
Following code allows for loitering.
public String pop() {
return s[--N];
}
Following code avoids loitering, so garbage collector can reclaim memory for an object only if no outstanding references.
public String pop() {
String item = s[--N];
s[N] = null;
return item;
}
Bags, Queues, and Stacks
resizing arrays
stack: resizing-array implementation
Problem: requiring client to provide capacity does not implement API!
Q: How to grow and shrink array?
First try:
push(): increase size of arrays[]by1.pop(): decrease size of arrays[]by1.
Too expensive!
stack: resizing-array implementation
Resizing by increasing size of array by 1:
- Need to copy a items to a new array, for each operation
- Array accesses to insert first \(N\) items is \(\underbrace{N}_1 + \underbrace{(2+4+\ldots+2(N-1))}_{2(k-1)} \texttilde N^2\)
- \(1\) array access per push
- \(2(k-1)\) array accesses to expand to size \(k\), ignoring cost to create new array
- Infeasible for large \(N\)
stack: resizing-array implementation
Challenge: Ensure that array resizing happens infrequently
stack: resizing-array implementation
Q. How to grow array?
A. If array is full, create a new array of twice the size, and copy items. (twice = repeated doubling)
public ResizingArrayStackOfStrings() {
s = new String[1];
}
public void push(String item) {
if(N == s.length) resize(2 * s.length);
s[N++] = item;
}
private void resize(int capacity) {
String[] copy = new String[capacity];
for(int i = 0; i < N; i++) copy[i] = s[i];
s = copy;
}
stack: resizing-array implementation
Array accesses to insert first \(N = 2^i\) items: \(\underbrace{N}_1 + \underbrace{(2+4+8+\ldots+N)}_k \texttilde 3N\)
- \(1\) array access per push
- \(k\) array accesses to double to size \(k\), ignoring cost to create new array
stack: resizing-array implementation
Q: How to shrink array?
First try:
push(): double size ofs[]when array is fullpop(): halve size of arrays[]when array is one-half full
Too expensive in worst case
- Consider push-pop-push-pop-... sequence when array is full
- Each operation takes time proportional to \(N\)
stack: resizing-array implementation



stack: resizing-array implementation
Q. How to shrink array?
Efficient solution:
push(): double size of arrays[]when array is fullpop(): halve size of arrays[]when array is one-quarter full
public String pop() {
String item = s[--N];
s[N] = null;
if(N > 0 && N == s.length/4) resize(s.length/2);
return item;
}
Invariant: Array is between 25% and 100% full
stack resizing-array: performance
- Amortized analysis
- Starting from an empty data structure, average running time per operation over a worst-case sequence of operations
Proposition: starting from an empty stack, any sequence of \(M\) push and pop operations takes time proportional to \(M\)
Order of growth of running time for resizing stack with \(N\) items:
| operation | best | worst | amortized |
|---|---|---|---|
construct |
\(1\) | \(1\) | \(1\) |
push |
\(1\) | \(N\) | \(1\) |
pop |
\(1\) | \(N\) | \(1\) |
size |
\(1\) | \(1\) | \(1\) |
\(N\) for push and pop because of doubling and halving operations.
stack resizing-array: memory usage
Proposition: uses between \(\texttilde 8N\) and \(\texttilde 32N\) bytes to represent a stack with \(N\) items
- \(\texttilde 8N\) when full
- \(\texttilde 32N\) when one-quarter full
public class ResizingArrayStackOfStrings {
private String[] s; // 8 bytes * array size
private int N = 0;
// ...
}
Remark: this accounts for the memory for the stack, but not the memory for strings themselves, which the client owns.
stack: resizing array vs. linked list
Tradeoffs: can implement a stack with either resizing array or linked list; client can use interchangeably. Which one is better?
Linked-list implementation
- Every operation takes constant time in the worst case
- Uses extra time and space to deal with the links
Resizing-array implementation
- Every operation takes constant amortized time
- Less wasted space


Bags, Queues, and Stacks
queues
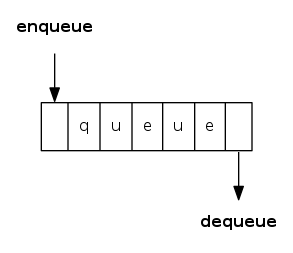
Queue API

How to implement queue with linked list?
A. Can't be done efficiently with a singly-linked list?
B.

C.
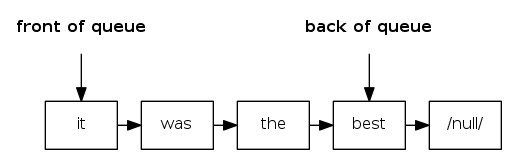
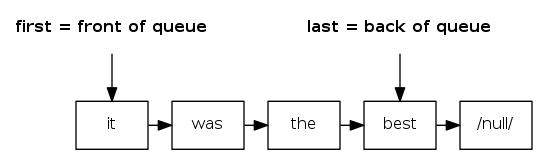
Queue: linked-list implementation
- Maintain one pointer
firstto first node in singly-linked list - Maintain another pointer
lastto last node - Dequeue from
first - Enqueue after
last
queue dequeue: linked-list implementation
public String dequeue() {
String item = first.item; // save item to return
first = first.next; // delete first node
return item; // return saved item
}
Remark: Identical code to linked-list stack pop
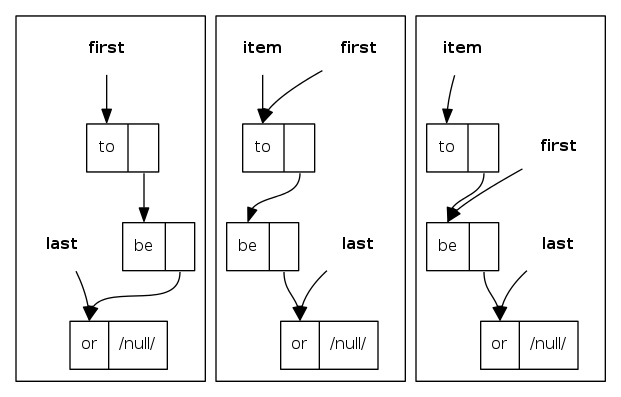
queue enqueue: linked-list implementation
public String enqueue(String item) {
Node oldlast = last; // save a link to the last node
last = new Node(); // create a new node for end
last.item = item;
oldlast.next = last; // link new node to end of list
}

queue: linked-list implementation in java
public class LinkedQueueOfStrings {
private Node first, last;
private class Node { /* same as in LinkedStackOfStrings */ }
public boolean isEmpty() { return first == null; }
public void enqueue(String item) {
Node oldlast = last;
last = new Node();
last.item = item;
last.next = null;
if(isEmpty()) first = last; // handle special case
else oldlast.next = last; // for empty queue
}
public String dequeue() {
String item = first.time
first = first.next;
if(isEmpty()) last = null; // handle special case...
return item;
}
}
how to implement a fixed-capacity queue with an array?
A. Can't be done efficiently with an array.
B.

C.
how to implement a fixed-capacity queue with an array?
A. Can't be done efficiently with an array.
B.
C.
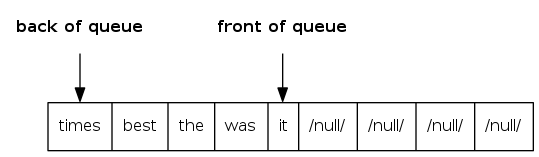
D. Either B or C
queue: resizing-array implementation
- Use array
q[]to store items in queue enqueueadds new item atq[tail]dequeueremoves item fromq[head]- Update
headandtailmodulo thecapacity - Add resizing array
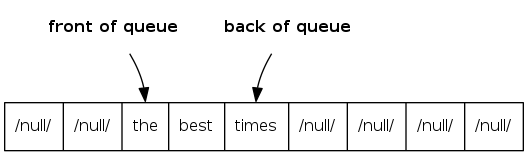
Q: How to resize?
Bags, Queues, and Stacks
generics
parameterized stack
We implemented StackOfStrings
We also want StackOfURLs, StackOfInts, StackOfVans, ...
Attempt 1: Implement a separate stack class for each type
- Rewriting code is tedious and error-prone
- Maintaining cut-and-pasted code is tedious and error-prone
Unfortunately, this was most reasonable approach in Java until 1.5!
parameterized stack
We implemented StackOfStrings
We also want StackOfURLs, StackOfInts, StackOfVans, ...
Attempt 2: Implement a stack with items of type Object
- Casting is required in client
- Casting is error-prone: run-time error if types mismatch
StackOfObjects s = new StackOfObjects(); Apple a = new Apple(); Banana b = new Banana(); s.push(a); s.push(b); a = (Apple) (s.pop()); // run-time error!
parameterized stack
We implemented StackOfStrings
We also want StackOfURLs, StackOfInts, StackOfVans, ...
Attempt 3: Java generics
- Avoid casting in client
- Discover type mismatch errors at compile-time instead of run-time
Stack<Apple> s = new Stack<Apple>(); // ^^^^^ ^^^^^ type parameter Apple a = new Apple(); Banana b = new Banana(); s.push(a); s.push(b); // compile-time error a = s.pop();
Guiding principles: welcome compile-time errors; avoid run-time errors
Generic stack: linked-list implementation
public class LinkedStackOfStrings {
private Node first = null;
private class Node { // private inner class
String item; // (access modifiers for instance
Node next; // variables don't matter)
}
public boolean isEmpty() { return first == null; }
public void push(String item) {
Node oldfirst = first;
first = new Node();
first.item = item;
first.next = oldfirst;
}
public String pop() {
String item = first.item;
first = first.next;
return item;
}
}
Generic stack: linked-list implementation
public class LinkedStack<Item> {
private Node first = null;
private class Node { // private inner class
Item item; // (access modifiers for instance
Node next; // variables don't matter)
}
public boolean isEmpty() { return first == null; }
public void push(Item item) {
Node oldfirst = first;
first = new Node();
first.item = item;
first.next = oldfirst;
}
public Item pop() {
Item item = first.item;
first = first.next;
return item;
}
}
generic stack: array implementation
public class FixedCapacityStackOfStrings {
private String[] s;
private int N = 0;
public FixedCapacityStackOfStrings(int capacity) {
s = new String[capacity];
}
public boolean isEmpty() { return N == 0; }
public void push(String item) { s[N++] = item; }
public String pop() { return s[--N]; }
}
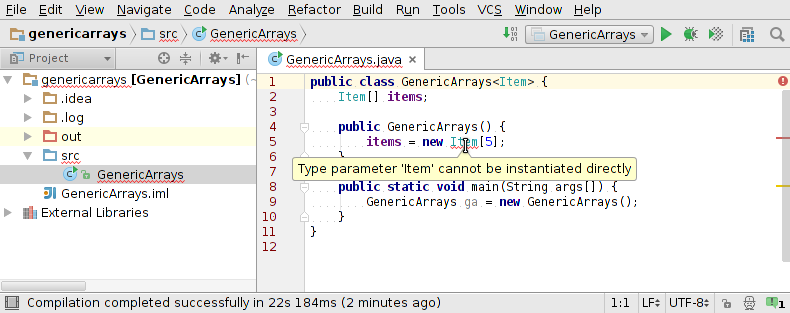
generic stack: array implementation
public class FixedCapacityStack<Item> {
private Item[] s;
private int N = 0;
public FixedCapacityStackOfStrings(int capacity) {
s = new Item[capacity]; // <- not allowed in Java :(
}
public boolean isEmpty() { return N == 0; }
public void push(Item item) { s[N++] = item; }
public Item pop() { return s[--N]; }
}
Except line 6 (generic array creation) is not allowed in Java :(
generic stack: array implementation
public class FixedCapacityStack<Item> {
private Item[] s;
private int N = 0;
public FixedCapacityStackOfStrings(int capacity) {
s = (Item[]) new Object[capacity]; // ugly cast :(
}
public boolean isEmpty() { return N == 0; }
public void push(Item item) { s[N++] = item; }
public Item pop() { return s[--N]; }
}
A (ugly) cast will "fix" the problem :|
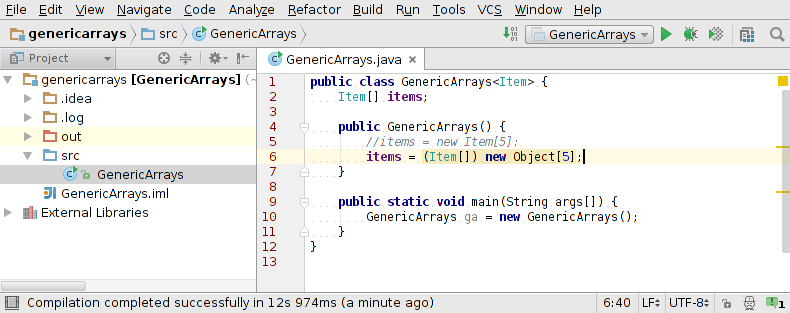
Unchecked cast
May get a compiler warning
$ javac GenericArrays.java
Note: GenericArrays.java uses unchecked or unsafe operations.
Note: Recompile with -Xlint:unchecked for details.
$ javac -Xlint:unchecked GenericArrays.java
GenericArrays.java:6: warning: [unchecked] unchecked cast
items = (Item[]) new Object[5];
^
required: Item[]
found: Object[]
where Item is a type-variable:
Item extends Object declared in class GenericArrays
1 warning
Q: Why does Java make me cast (or use reflection)?
Short answer: Backward compatibility.
Long answer: Need to learn about type erasure and covariant arrays.
Generic data types: autoboxing
Q: What to do about primitive types? (int, double, boolean, etc.)
Wrapper type
- Each primitive has a wrapper object type
- ex:
Integerforint,Doublefordouble,Booleanforboolean, etc.
- Autoboxing
- Automatic cast between a primitive type and its wrapper
Stack<Integer> s = new Stack<Integer>(); s.push(17); // s.push(Integer.valueOf(17)); int a = s.pop(); // int a = s.pop().intValue();
Bottom line: Client code can use generic stack for any type of data
Bags, Queues, and Stacks
iterators
iteration
Design challenge: Support iteration over stack items by client, without revealing the internal representation of the stack.
Java solution: Make stack implement the java.lang.Iterable interface
iteration
Q. What is an Iterable?
A. Has a method that returns an Iterator.
Q. What is an Iterator?
A. Has methods hasNext() and next().
// java.lang.Iterable interface
public interface Iterable<Item> {
Iterator<Item> iterator();
}
// java.util.Iterator interface
public interface Iterator<Item> {
boolean hasNext();
Item Next();
void remove(); // optional; use at your own risk
}
iteration
Q. Why make data structures Iterable?
A. Java support elegant client code.
// "foreach" statement (shorthand)
for(String s : stack) {
StdOut.println(s);
}
// equivalent code (longhand)
Iterator<String> i = stack.iterator();
while(i.hasNext()) {
String s = i.next();
StdOut.println(s);
}
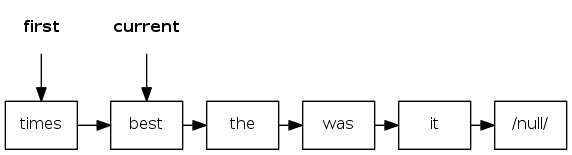
stack iterator: linked-list implementation
Version 1: named Iterator class
import java.util.Iterator; // <- must import this!
public class Stack<Item> implements Iterable<Item> {
/* ... */
public Iterator<Item> iterator() { return new ListIterator(); }
private class ListIterator implements Iterator<Item> {
private Node<Item> current = first;
public boolean hasNext() { return current != null; }
public void remove() { /* not supported */ }
public Item next() {
Item item = current.item;
current = current.next;
return item;
}
}
}

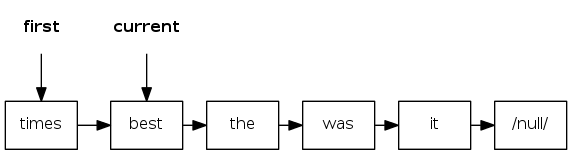
stack iterator: linked-list implementation
Version 2: unnamed Iterator class
import java.util.Iterator; // <- must import this!
public class Stack<Item> implements Iterable<Item> {
/* ... */
public Iterator<Item> iterator() {
return new Iterator<Item>() {
private Node<Item> current = first;
public boolean hasNext() { return current != null; }
public void remove() { /* not supported */ }
public Item next() {
Item item = current.item;
current = current.next;
return item;
}
};
}
}
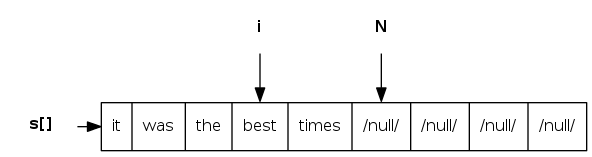
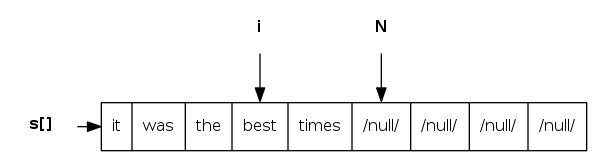
stack iterator: array implementation
Version 1: named Iterator class
public class Stack<Item> implements Iterable<Item> {
/* ... */
public Iterator<Item> iterator() {
return new ReverseArrayIterator();
}
private class ReverseArrayIterator implements Iterator<Item> {
private int i = N;
public boolean hasNext() { return i > 0; }
public void remove() { /* not supported */ }
public Item next() { return s[--i]; }
}
}
iteration: concurrent modification
Q. What if client modifies the data structure while iterating?
A. A fail-fast iterator throws a java.util.ConcurrentModificationException.
// concurrent modification :( for(String s : stack) stack.push(s);
Q. How to detect?
A. Simple!
- Count total number of
push()andpop()operations inStack - Save counts in
Iteratorsubclass upon creation - If, when calling
next()andhasNext(), the current count and saved count do not equal (client calledpushorpop), throw exception
Bags, Queues, and Stacks
applications
java collections library
List interface: java.util.List is API for a sequence of items

Implementations: java.util.ArrayList uses resizing array; java.util.LinkedList uses linked list.
Caveat: only some operations are efficient!
java collections library
java.util.Stack
- Supports
push(),pop(), and iteration - Extends
java.util.Vector, which implementsjava.util.Listinterface from previous slide, includingget()andremove() - Bloated and poorly-designed API (why?)
java collections library
Java 1.3 bug report (June 27, 2001)
“The iterator method on java.util.Stack iterates through a Stack from the bottom up. One would think that it should iterate as if it were popping off the top of the Stack.
”
Status (closed, will not fix)
“It was an incorrect design decision to have Stack extend Vector ("is-a" rather than "has-a"). We sympathize with the submitter but cannot fix this because of compatibility.
”
java collections library
java.util.Stack
java.util.Queue: An interface, not an implementation of a queue
Best practices: use provided implementations of Stack, Queue, and Bag
War story
Generate random tile locations in \(N\)-by-\(N\) HexBoard
- Alice
- Pick
row,colat random; if already set, repeat - Takes \(\texttilde c_1 N^2\) seconds
- Pick
- Bob
- Create a
java.util.ArrayListof \(N^2\) unset tile locations - Pick an index at random and delete
- Takes \(\texttilde c_2 N^4\) seconds
- Create a
“Why is my program so slow?
”
War story
Lesson: Don't use a library until you understand its API!
This course: Can't use a library until we've implemented it in class
stack applications
- Parsing in a compiler
- Java virtual machine
- Undo in a word processor
- Back button in a web browser
- PostScript language for printers
- Implementing function calls in a compiler
- ...
function calls
How a compiler implements a function
- Function call: push local environment and return address
- Return: pop return address and local environment
Recursive function: Function that calls itself
Note: Can always use an explicit stack to remove recursion
function calls
Recursion example: greatest common divisor
static int gcd(int p, int q) {
if(q == 0) return p;
return gcd(q, p % q);
}
gcd(216, 192) // stack: p=216, q=192
gcd(192, 24) // stack: 216, 192, p=192, q=24
gcd(24, 0) // stack: 216, 192, 192, 24, p=24, q=0
<- 24 // stack: 216, 192, 192, 24, ret=24
<- 24 // stack: 216, 192, ret=24
<- 24 // stack: ret=24
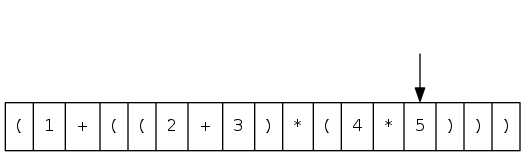
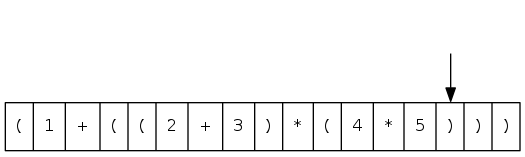
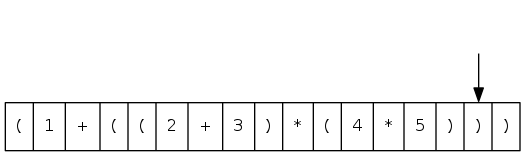
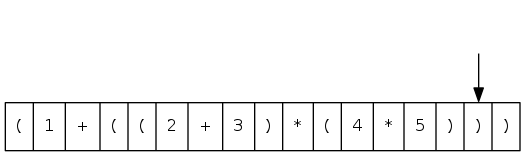
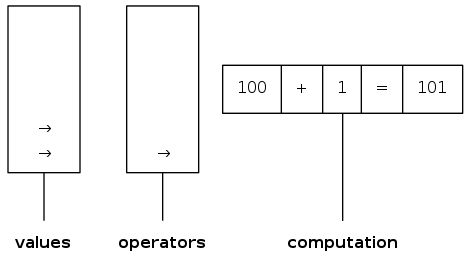
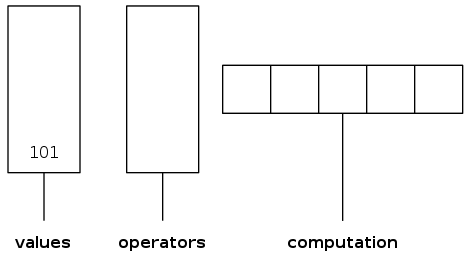
arithmetic expression evaluation
Goal: evaluate infix expressions
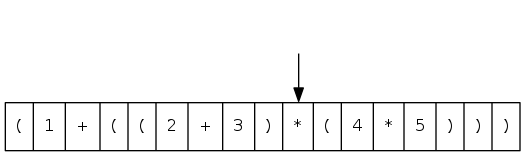
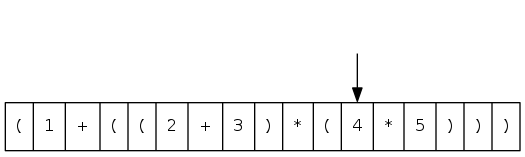
( 1 + ( ( 2 + 3 ) * ( 4 * 5 ) ) )
^ operand ^ operator
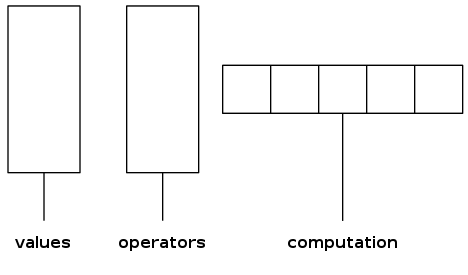
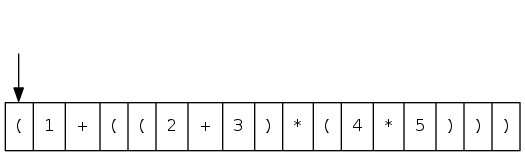
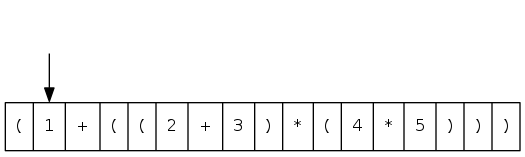
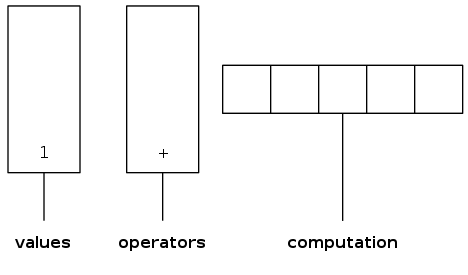
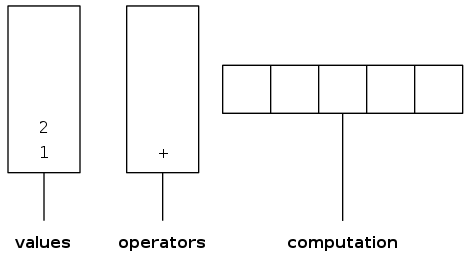
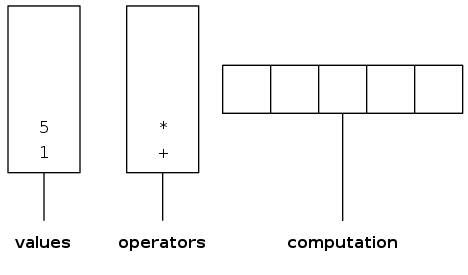
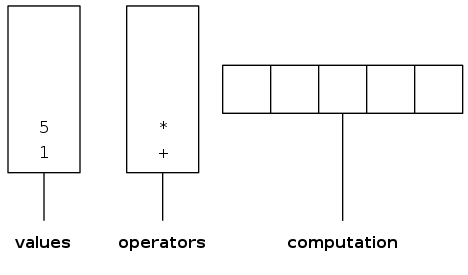
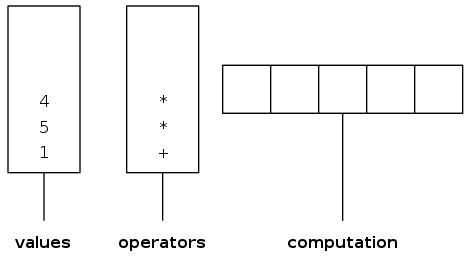
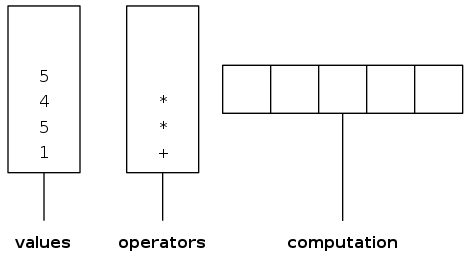
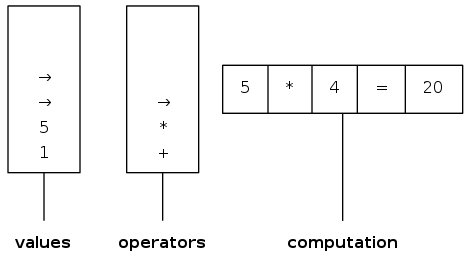
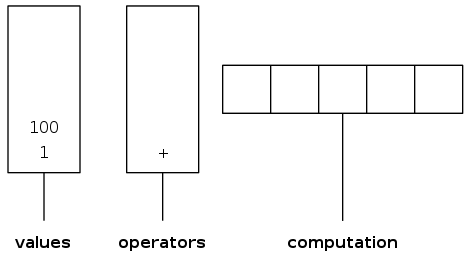
Two-stack algorithm (E. W. Dijkstra)
- Value: push onto the value stack
- Operator: push onto the operator stack
- Left parenthesis: ignore
- Right parenthesis: pop operator and two values, and push to operand stack the result of applying operator on values
Context: an interpreter!
Dijkstra's two-stack algorithm demo

infix expression (fully parenthesized)

Dijkstra's two-stack algorithm demo
infix expression (fully parenthesized)
Dijkstra's two-stack algorithm demo

infix expression (fully parenthesized)
Dijkstra's two-stack algorithm demo

infix expression (fully parenthesized)

Dijkstra's two-stack algorithm demo
infix expression (fully parenthesized)

Dijkstra's two-stack algorithm demo

infix expression (fully parenthesized)

Dijkstra's two-stack algorithm demo
infix expression (fully parenthesized)
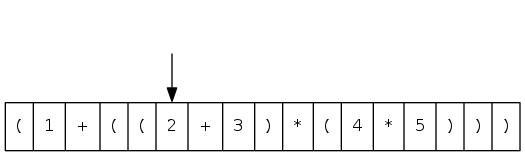
Dijkstra's two-stack algorithm demo

infix expression (fully parenthesized)

Dijkstra's two-stack algorithm demo

infix expression (fully parenthesized)
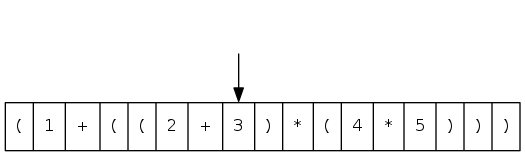
Dijkstra's two-stack algorithm demo

infix expression (fully parenthesized)

Dijkstra's two-stack algorithm demo
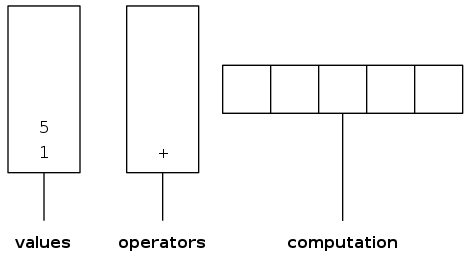
infix expression (fully parenthesized)

Dijkstra's two-stack algorithm demo
infix expression (fully parenthesized)
Dijkstra's two-stack algorithm demo
infix expression (fully parenthesized)

Dijkstra's two-stack algorithm demo

infix expression (fully parenthesized)
Dijkstra's two-stack algorithm demo
infix expression (fully parenthesized)

Dijkstra's two-stack algorithm demo
infix expression (fully parenthesized)
Dijkstra's two-stack algorithm demo
infix expression (fully parenthesized)
Dijkstra's two-stack algorithm demo

infix expression (fully parenthesized)

Dijkstra's two-stack algorithm demo

infix expression (fully parenthesized)
Dijkstra's two-stack algorithm demo
infix expression (fully parenthesized)
Dijkstra's two-stack algorithm demo
infix expression (fully parenthesized)

Dijkstra's two-stack algorithm demo
infix expression (fully parenthesized)
Dijkstra's two-stack algorithm demo

infix expression (fully parenthesized)
arithmetic expression evaluation
public class Evaluate {
public static void main(String[] args) {
Stack<String> ops = new Stack<String>();
Stack<Double> vals = new Stack<Double>();
while(!StdIn.isEmpty()) {
String s = StdIn.readString();
if (s.equals("(")) ;
else if(s.equals("+")) ops.push(s);
else if(s.equals("*")) ops.push(s);
else if(s.equals(")")) {
String op = ops.pop();
if (op.equals("+"))
vals.push(vals.pop() + vals.pop());
else if(op.equals("*"))
vals.push(vals.pop() * vals.pop());
} else vals.push(Double.parseDouble(s));
}
StdOut.println(vals.pop());
}
}
$ java Evaluate ( 1 + ( ( 2 + 3 ) * ( 4 * 5 ) ) ) 101.0
correctness
Q. Why correct?
A. When algorithm encounters an operator surrounded by two values within parentheses, it leaves the result on the value stack as if it was the original input.
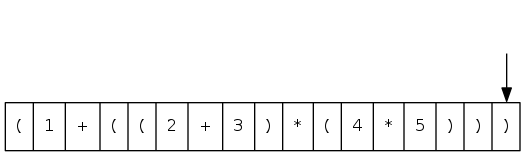
input: ( 1 + ( ( 2 + 3 ) * ( 4 * 5 ) ) )
processing: ( 1 + ( ( 2 + 3 ) ...
( 1 + ( 5 * ( 4 * 5 ) ...
( 1 + ( 5 * 20 ) ...
( 1 + 100 )
output: 101
Extensions: More ops, precedence order, associativity
stack-based programming languages
Observation 1: Dijkstra's two-stack algorithm computes the same value if the operator occurs after the two values
Observation 2: All the parentheses are redundant!
infix: ( 1 + ( ( 2 + 3 ) * ( 4 * 5 ) ) ) postfix: ( 1 ( ( 2 3 + ) ( 4 5 * ) * ) + ) no ()s: 1 2 3 + 4 5 * * + short: 1 2 3 + 4 5 * * +
Bottom line: Postfix or "reverse Polish" notation
Applications: Postscript, Forth, calculators, Java virtual machine, ...

