Union-Find
COS 265 - Data Structures & Algorithms
Union-Find
dynamic-connectivity problem
dynamic-connectivity problem
Given a set of \(N\) elements, support two operations:
- Connection command: directly connect two elements with an edge
- Connection query: is there a path connecting two elements?
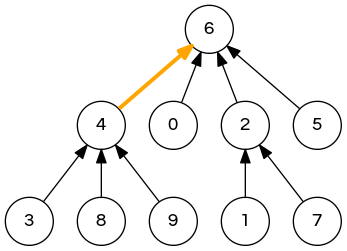
dynamic-connectivity problem
connect(4, 3) connect(3, 8) connect(6, 5) connect(9, 4) connect(2, 1) isConnected(8, 9) // true isConnected(5, 7) // false connect(5, 0) connect(7, 2) connect(6, 1) connect(1, 0) isConnected(5, 7) // true |
 |
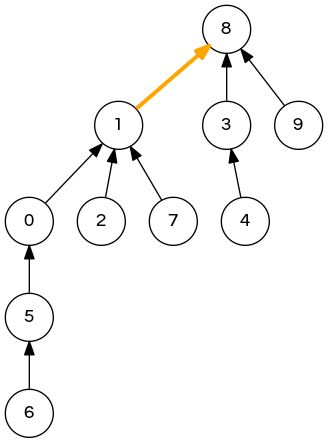
dynamic-connectivity problem
connect(4, 3) connect(3, 8) connect(6, 5) connect(9, 4) connect(2, 1) isConnected(8, 9) // true isConnected(5, 7) // false connect(5, 0) connect(7, 2) connect(6, 1) connect(1, 0) isConnected(5, 7) // true |
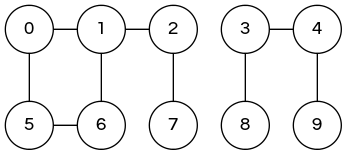 |
A larger connectivity example
Is there a path connecting cyan and pink elements?

A larger connectivity example
Is there a path connecting cyan and pink elements?

Yes.
Note: finding the path explicitly is a harder problem
modeling the elements
Applications involve manipulating elements of all types
- pixels in a digital photo
- computers in a network
- friends in a social network
- transistors in a computer chip
- elements in a mathematical set
- variable names in a Fortran program
- metallic sites in a composite system
modeling the elements
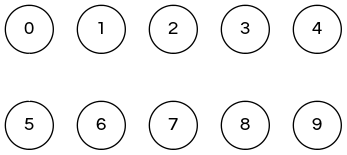
When programming, convenient to name elemenst 0 to N-1.
- use integers as array index
- suppress details not relevant to union-find
modeling the elements
We model "is connected to" as an equivalence relation:
- Reflexive:
pis connected top - Symmetric: if
pis connected toq, thenqis connected top - Transitive: if
pis connected toqandqis connected tor, thenpis connected tor
modeling the elements
- Connected component
- maximal set of elements that are mutually connected
|
3 disjoint sets / connected components \[ \{0\}\ \{1,4,5\}\ \{2,3,6,7\} \] |
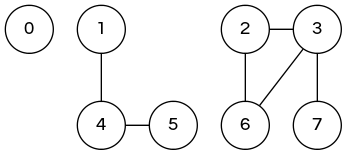 |
two core operations on disjoint sets
- Union
- replace set
pandqwith their union - Find
- in which set is element
p?
\[\{0\}\ \{1,4,5\}\ \{2,3,6,7\}\quad\Rightarrow\quad\{0\}\ \{1,2,3,4,5,6,7\}\]
find(5) != find(6) union(2, 5) // 3 disjoint sets -> 2 disjoint sets find(5) == find(6)
modeling dynamic-connectivity using u-f
How to model the dynamic-connectivity problem using union-find?
Maintain disjoint sets that correspond to connected components
union(2, 5)
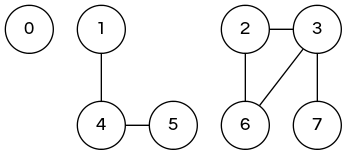 |
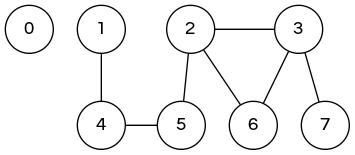 |
union-find data type (api)
Goal: design an efficient union-find data type
- number of elements \(N\) can be huge
- number of operations \(M\) can be huge
- union and find operations can be intermixed
public class UF {
UF(int N) // initialize union-find data structure with
// N singleton sets (0 to N-1)
void union(int p, int q) // merge sets containing elements
// p and q
int find(int p) // identifier for set containing
// element p (0 to N-1)
}
dynamic-connectivity client
- read in number of elements \(N\) from standard input
- repeat:
- read in pair of integers from standard input
- if they are not yet connected, connect them and print pair
public static void main(String[] args) {
int N = StdIn.readInt();
UF uf = new UF(N);
while(!StdIn.isEmpty()) {
int p = StdIn.readInt();
int q = StdIn.readInt();
if(uf.find(p) != uf.find(q)) {
uf.union(p, q);
StdOut.println(p + " " + q);
}
}
}
dynamic-connectivity client
Note with input below, lines 8, 12, and 13 are already connected and therefore will not print.
% more tinyUF.txt 10 4 3 3 8 6 5 9 4 2 1 8 9 5 0 7 2 6 1 1 0 6 7
Union-Find
quick find
quick-find (eager approach)
Data Structure
- Integer array
id[]of lengthN - Interpretation:
id[p]identifies the set containing elementp
\[ \{0,5,6\}\ \{1,2,7\}\ \{3,4,8,9\} \]
// 0 1 2 3 4 5 6 7 8 9
int [] id = {0,1,1,8,8,0,0,1,8,8};
// find(5) == 0
Q: How to implement find(p)?
quick-find (eager approach)
Data Structure
- Integer array
id[]of lengthN - Interpretation:
id[p]identifies the set containing elementp
\[ \{0,5,6\}\ \{1,2,7\}\ \{3,4,8,9\} \]
// 0 1 2 3 4 5 6 7 8 9
int [] id = {0,1,1,8,8,0,0,1,8,8};
// find(5) == 0
Q: How to implement find(p)?
A: Easy, just return id[p]
quick-find (eager approach)
Data Structure
- Integer array
id[]of lengthN - Interpretation:
id[p]identifies the set containing elementp
\[ \{0,5,6\}\ \{1,2,7\}\ \{3,4,8,9\} \Rightarrow \{0,1,2,5,6,7\}\ \{3,4,8,9\} \]
// 0 1 2 3 4 5 6 7 8 9
int [] id = {0,1,1,8,8,0,0,1,8,8};
union(6,1);
// id = ??
Q: How to implement union(p,q)?
quick-find (eager approach)
Data Structure
- Integer array
id[]of lengthN - Interpretation:
id[p]identifies the set containing elementp
\[ \{0,5,6\}\ \{1,2,7\}\ \{3,4,8,9\} \Rightarrow \{0,1,2,5,6,7\}\ \{3,4,8,9\} \]
// 0 1 2 3 4 5 6 7 8 9
int [] id = {0,1,1,8,8,0,0,1,8,8};
union(6,1);
// id = ??
Q: How to implement union(p,q)?
A: Change all entries whose identifier equals id[p] to id[q].
id = {1,1,1,8,8,1,1,1,8,8}
quick-find java implementation
public class QuickFindUF {
private int[] id;
public QuickFindUF(int N) {
// set id of each element to itself (N array accesses)
id = new int[N];
for(int i = 0; i < N; i++)
id[i] = i;
}
public int find(int p) {
// return the id of p (1 array access)
return id[p];
}
public void union(int p, int q) {
// change all entries with id[p] to id[q]
// (N+2 to 2N+2 array accesses)
int pid = id[p];
int qid = id[q];
for(int i = 0; i < id.length; i++) {
if(id[i] == pid) id[i] = qid;
}
}
}
quick-find is too slow
- Cost model
- Number of array accesses (for read or write)
| algorithm | initialize | union | find |
|---|---|---|---|
| quick-find | \(N\) | \(N\) | \(1\) |
Note: ignoring leading constant
Union is too expensive! Processing a sequence of \(N\) union operations on \(N\) elements takes more than \(N^2\) (quadratic) array accesses.
quadratic algorithms do not scale
Rough standard (for now)
- \(10^9\) operations per second
- \(10^9\) words of main memory
- touch all words in approximately 1 second
- a truism (roughly) since 1950!
Ex. Huge problem for quick-find
- \(10^9\) union commands on \(10^9\) elements
- quick-find takes more than \(10^{18}\) operations
- 30+ years of computer time!
quadratic algorithms do not scale
Quadratic algorithms don't scale with technology
- new computer may be 10x as fast
- but it has 10x as much memory \(\Rightarrow\) want to solve a problem that is 10x as big
- with quadratic algorithm, takes 10x as long!
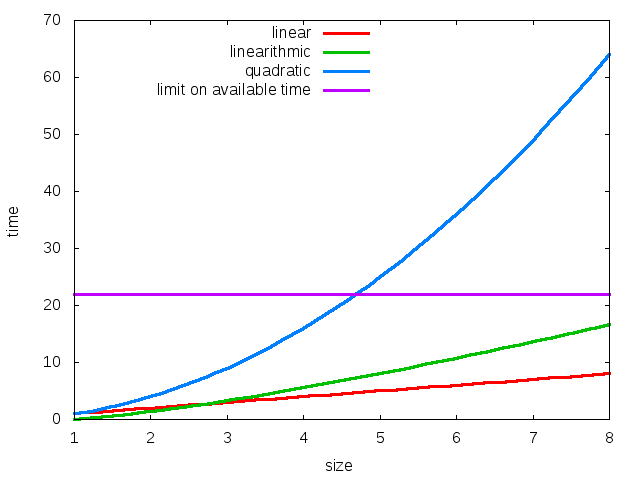
Union-Find
quick union
quick-union (lazy approach)
Data Structure
- Integer array
parent[]of lengthN, whereparent[i]is parent ofiin tree - Interpretation: elements in a tree corresponding to a set
quick-union (lazy approach)
\[ \{0\}\ \{1\}\ \{2,3,4,9\}\ \{5,6\}\ \{7\}\ \{8\} \]
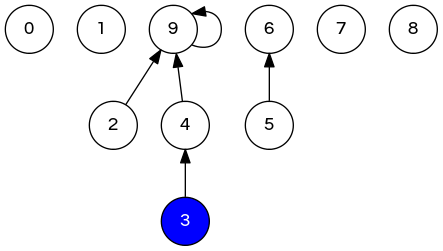
// 0 1 2 3 4 5 6 7 8 9
int [] id = {0,1,9,4,9,6,6,7,8,9};
// parent of 3 is 4, parent of 4 is 9, parent of 9 is 9
// root of 3 is 9
Q: How to implement find(p)?
quick-union (lazy approach)
\[ \{0\}\ \{1\}\ \{2,3,4,9\}\ \{5,6\}\ \{7\}\ \{8\} \]
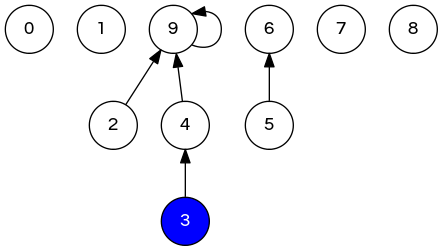
// 0 1 2 3 4 5 6 7 8 9
int [] id = {0,1,9,4,9,6,6,7,8,9};
// parent of 3 is 4, parent of 4 is 9, parent of 9 is 9
// root of 3 is 9
Q: How to implement find(p)?
A: Return root of tree containing p
quick-union (lazy approach)
\[ \ldots \{2,3,4,9\} \{5,6\} \ldots \Rightarrow \ldots \{2,3,4,5,6,9\} \ldots \]
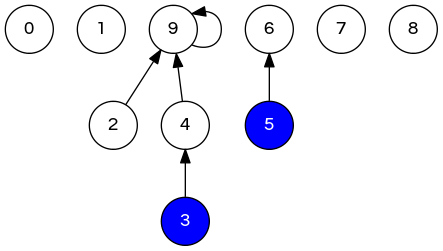
// 0 1 2 3 4 5 6 7 8 9
int [] id = {0,1,9,4,9,6,6,7,8,9};
union(3, 5)
// id = ???
Q: How to implement union(p,q)?
quick-union (lazy approach)
\[ \ldots \{2,3,4,9\} \{5,6\} \ldots \Rightarrow \ldots \{2,3,4,5,6,9\} \ldots \]
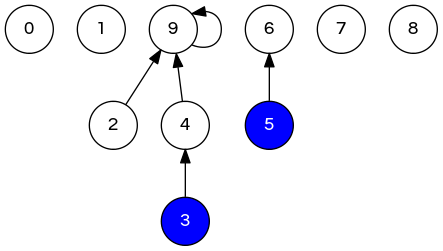
// 0 1 2 3 4 5 6 7 8 9
int [] id = {0,1,9,4,9,6,6,7,8,9};
union(3, 5)
// id = ???
Q: How to implement union(p,q)?
A: Set parent of p's root to parent of q's root.
quick-union (lazy approach)
\[ \ldots \{2,3,4,9\} \{5,6\} \ldots \Rightarrow \ldots \{2,3,4,5,6,9\} \ldots \]
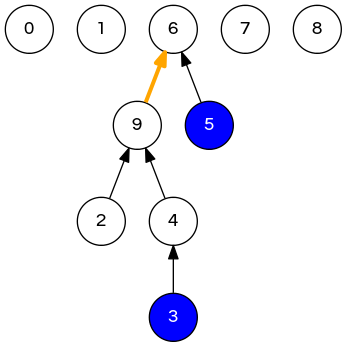
// 0 1 2 3 4 5 6 7 8 9
int [] id = {0,1,9,4,9,6,6,7,8,9};
union(3, 5)
// id = {0,1,9,4,9,6,6,7,8,6}
// ^ only one value changes!
quick-union demo
union(4,3) union(3,8) union(6,5) union(9,4) union(2,1) isConnected(8,9) !isConnected(5,4) union(5,0) union(7,2) union(6,1) union(7,3)
quick-union demo
int [] id = {0,1,2,3,4,5,6,7,8,9};
union(4,3); // <- next step

quick-union demo
union(4,3); // 0 1 2 3 4 5 6 7 8 9 => 0 1 2 3 3 5 6 7 8 9 union(3,8); // <- next step
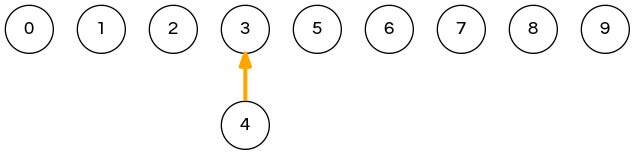
quick-union demo
union(3,8); // 0 1 2 3 3 5 6 7 8 9 => 0 1 2 8 3 5 6 7 8 9 union(6,5); // <- next step

quick-union demo
union(6,5); // 0 1 2 8 3 5 6 7 8 9 => 0 1 2 8 3 5 5 7 8 9 union(9,4); // <- next step
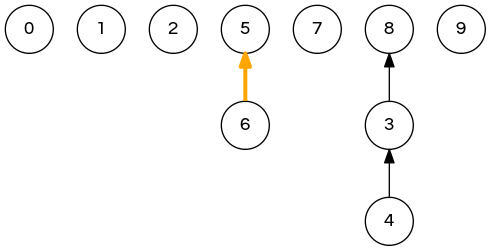
quick-union demo
union(9,4); // 0 1 2 8 3 5 5 7 8 9 => 0 1 2 8 3 5 5 7 8 8 union(2,1); // <- next step
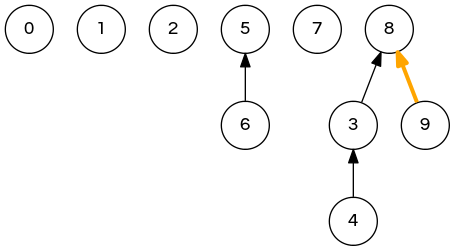
quick-union demo
union(2,1); // 0 1 2 8 3 5 5 7 8 8 => 0 1 1 8 3 5 5 7 8 8 union(5,0); // <- next step
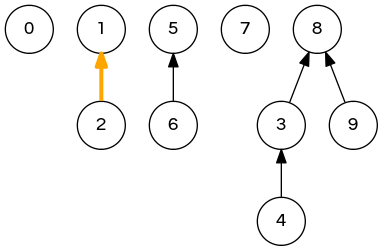
quick-union demo
union(5,0); // 0 1 1 8 3 5 5 7 8 8 => 0 1 1 8 3 0 5 7 8 8 union(7,2); // <- next step
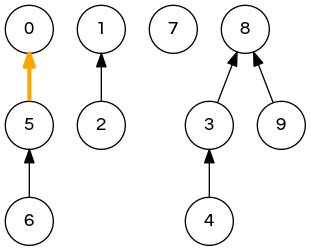
quick-union demo
union(7,2); // 0 1 1 8 3 0 5 7 8 8 => 0 1 1 8 3 0 5 1 8 8 union(6,1); // <- next step
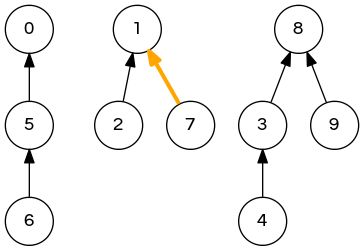
quick-union demo
union(6,1); // 0 1 1 8 3 0 5 1 8 8 => 1 1 1 8 3 0 5 1 8 8 union(7,3); // <- next step
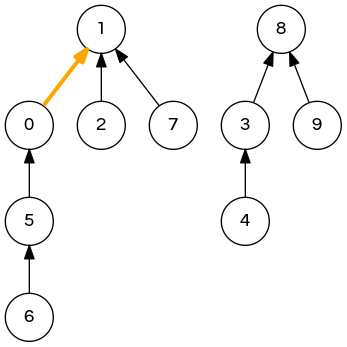
quick-union demo
union(7,3); // 1 1 1 8 3 0 5 1 8 8 => 1 8 1 8 3 0 5 1 8 8 // all done!
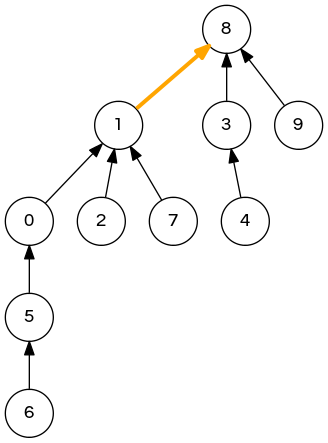
quick-union java implementation
public class QuickUnionUF {
private int[] parent;
public QuickUnionUF(int N) {
// set parent of each element to itself
// N array accesses
parent = new int[N];
for(int i = 0; i < N; i++)
parent[i] = i;
}
public int find(int p) {
// chase parent pointers until reach root
// depth of p array accesses
while(p != parent[p])
p = parent[p];
return p;
}
public void union(int p, int q) {
// change root of p to point to root of q
// depth of p and q array accesses
int i = find(p);
int j = find(q);
parent[i] = j;
}
}
quick-union is also too slow
- Cost model
- Number of array accesses (for read or write)
| algorithm | initialize | union | find |
|---|---|---|---|
| quick-find | \(N\) | \(N\) | \(1\) |
| quick-union | \(N\) | \(N^\dagger\) | \(N\) |
\(\dagger\) includes cost of finding two roots
Note: analyzed quick-union for worst case
quick-union is also too slow
|
Quick-find defect
Quick-union defect
// worst-case input union(0,1); union(0,2); union(0,3); union(0,4); |
 |
Union-find
improvements
improvement 1: weighting
Weighted quick-union
- Modify quick-union to avoid tall trees
- Keep track of size of each tree (number of elements)
- Always link root of smaller tree to root of larger tree
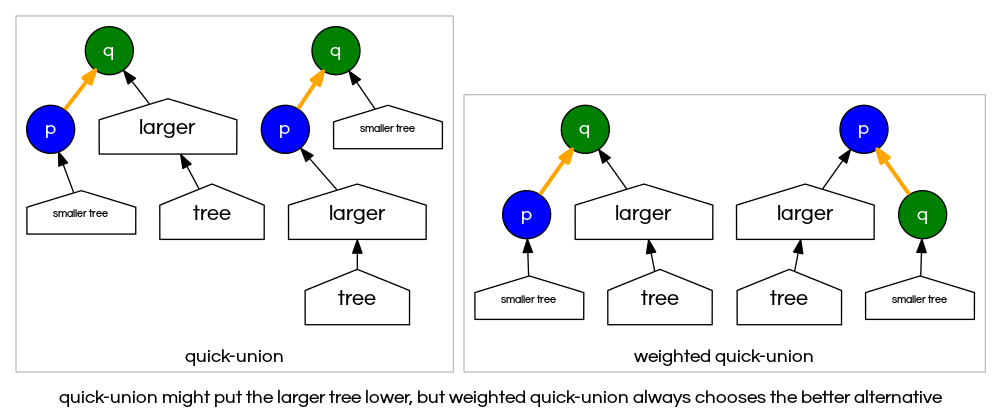
weighted quick-union quiz
Suppose that the parent[] array during weighted quick union is
// 0 1 2 3 4 5 6 7 8 9
int [] parent = {0,0,0,0,0,0,7,8,8,8};
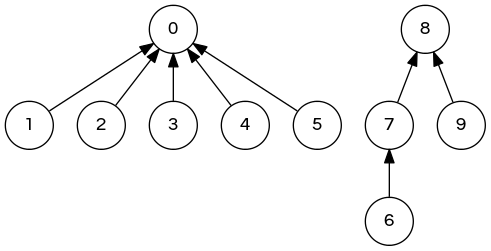
Which parent[] entry changes during union(2,6)?
A. parent[0]
B. parent[2]
C. parent[6]
D. parent[8]
weighted quick-union demo
union(4,3) union(3,8) union(6,5) union(9,4) union(2,1) union(5,0) union(7,2) union(6,1) union(7,3)
weighted quick-union demo
int [] id = {0,1,2,3,4,5,6,7,8,9};
union(4,3); // <- next step

weighted quick-union demo
union(4,3); // 0 1 2 3 4 5 6 7 8 9 => 0 1 2 4 4 5 6 7 8 9 union(3,8); // <- next step
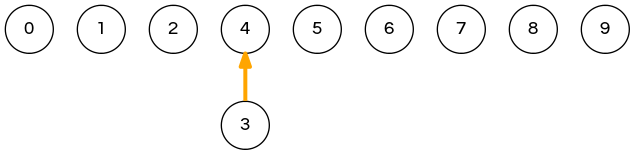
weighted quick-union demo
union(3,8); // 0 1 2 4 4 5 6 7 8 9 => 0 1 2 4 4 5 6 7 4 9 union(6,5); // <- next step
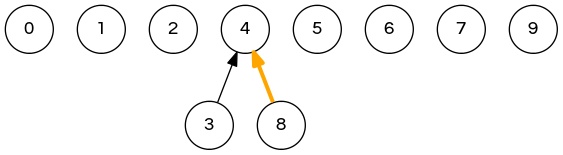
weighted quick-union demo
union(6,5); // 0 1 2 4 4 5 6 7 4 9 => 0 1 2 4 4 6 6 7 4 9 union(9,4); // <- next step
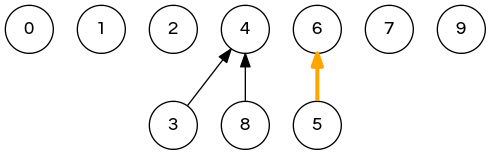
weighted quick-union demo
union(9,4); // 0 1 2 4 4 6 6 7 4 9 => 0 1 2 4 4 6 6 7 4 4 union(2,1); // <- next step
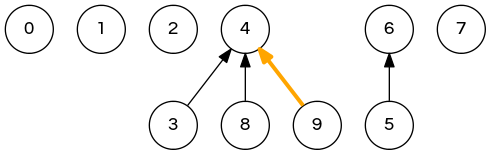
weighted quick-union demo
union(2,1); // 0 1 2 4 4 6 6 7 4 4 => 0 2 2 4 4 6 6 7 4 4 union(5,0); // <- next step
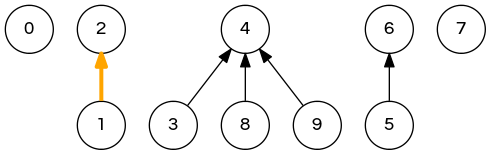
weighted quick-union demo
union(5,0); // 0 2 2 4 4 6 6 7 4 4 => 6 2 2 4 4 6 6 7 4 4 union(7,2); // <- next step
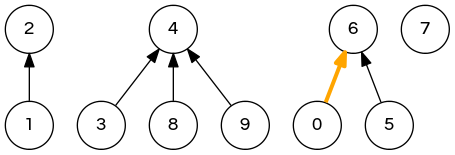
weighted quick-union demo
union(7,2); // 6 2 2 4 4 6 6 7 4 4 => 6 2 2 4 4 6 6 2 4 4 union(6,1); // <- next step
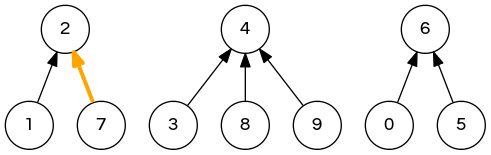
weighted quick-union demo
union(6,1); // 6 2 2 4 4 6 6 2 4 4 => 6 2 6 4 4 6 6 2 4 4 union(7,3); // <- next step
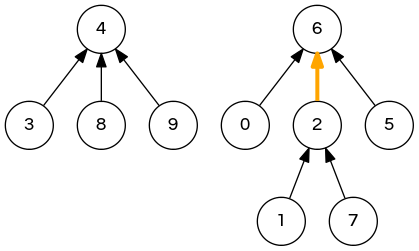
weighted quick-union demo
union(7,3); // 6 2 6 4 4 6 6 2 4 4 => 6 2 6 4 6 6 6 2 4 4 // all done!
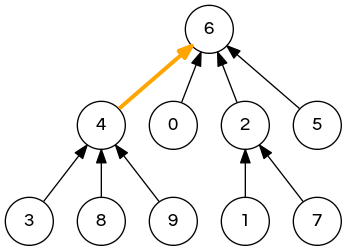
weighted quick-union demo
|
quick-union
|
weighted quick-union
|
quick-union vs. weighted quick-union
A larger example: 100 sites, 88 union() operations
quick-union, average distance to root = 5.11
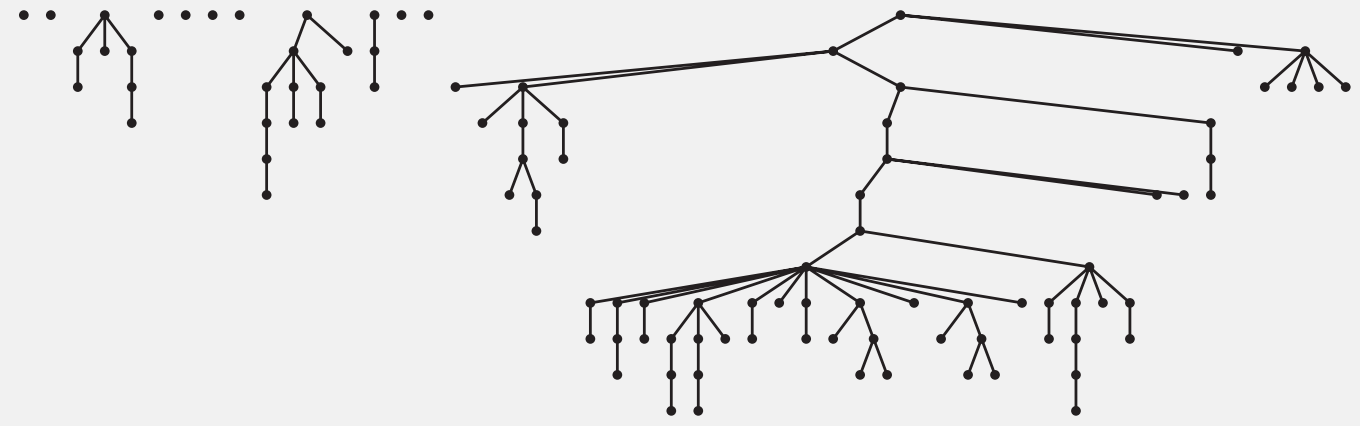
weighted quick-union, average distance to root: 1.52

weighted quick-union java implementation
Data structure: same as quick-union, but maintain extra array size[i] to count number of elements in the tree rooted at i, initially set to 1.
Find: identical to quick-union
Union: modify quick-union to:
- link root of smaller tree to root of larger tree
- update the
size[]array
int i = find(p);
int j = find(q);
if(i == j) return;
if(size[i] < size[j]) { parent[i] = j; size[j] += size[i]; }
else { parent[j] = i; size[i] += size[j]; }
weighted quick-union analysis
Running time
- Find: takes time proportional to depth of
p - Union: takes constant time, given two roots.
Proposition: depth of any node \(\textsf{x}\) is at most \(\lg N\) (in computer science, \(\lg\) means base-2 logarithm)
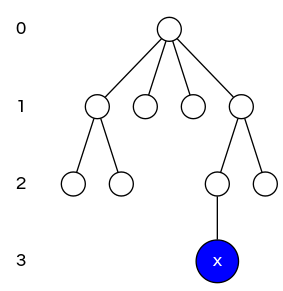 |
\[N = 10\] \[\text{depth}(\textsf{x}) \leq \lg N \approx 3.32\] |
weighted quick-union analysis
Proposition: depth of any node \(\textsf{x}\) is at most \(\lg N\) (in computer science, \(\lg\) means base-2 logarithm)
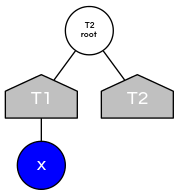
Proof: What causes the depth of element \(\textsf{x}\) to increase? Increase by 1 when root of tree \(\textsf{T1}\) containing \(\textsf{x}\) is linked to root of tree \(\textsf{T2}\).
- The size of the tree containing \(\textsf{x}\) at least doubles since \(|\textsf{T2}| \geq |\textsf{T1}|\).
- Size of tree containing \(\textsf{x}\) can double at most \(\lg N\) times. Why?
weighted quick-union analysis
| algorithm | initialize | union | find |
|---|---|---|---|
| quick-find | \(N\) | \(N\) | \(1\) |
| quick-union | \(N\) | \(N^\dagger\) | \(N\) |
| weighted QU | \(N\) | \(\lg N^\dagger\) | \(\lg N\) |
\(\dagger\) includes cost of finding two roots
Note: analyzed quick-union for worst case
summary
Key point: weighted quick-union makes it possible to solve problems that could not otherwise be addressed.
| algorithm | worst-case time |
|---|---|
| quick-find | \(M N\) |
| quick-union | \(M N\) |
| weighted QU | \(N + M \log N\) |
| QU + path compression | \(N + M \log N\) |
| weighted QU + path compression | \(N + M \lg^* N\) |
Order of growth for \(M\) union-find operations on a set of \(N\) elements
Example: \(10^9\) unions and finds with \(10^9\) elements
- WQUPC reduces time from 30 years to 6 seconds
- Supercomputer won't help much; good algorithm enables solution
Union-Find
applications
Union-find applications
- percolation
- games (Go, Hex)
- least common ancestor
- dynamic-connectivity problem
- equivalence of finite state automata
- Hoshen-Kopelman algorithm in physics
- Hinley-Milner polymorphic type inference
- Kruskal's minimum spanning tree algorithm
- Compiling equivalence statements in Fortran
- morphological attribute openings and closings
- Matlab's
bwlabel()function in image processing
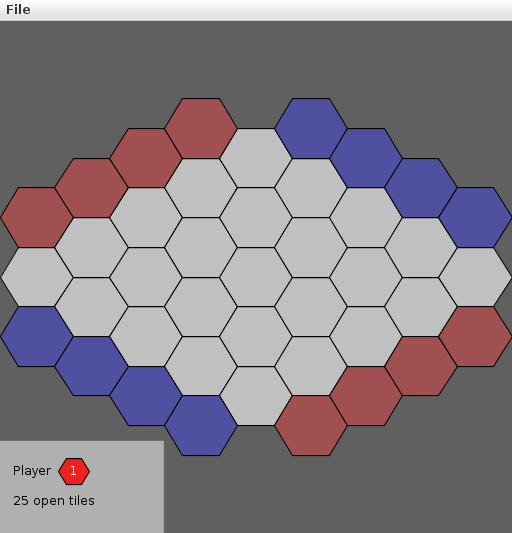
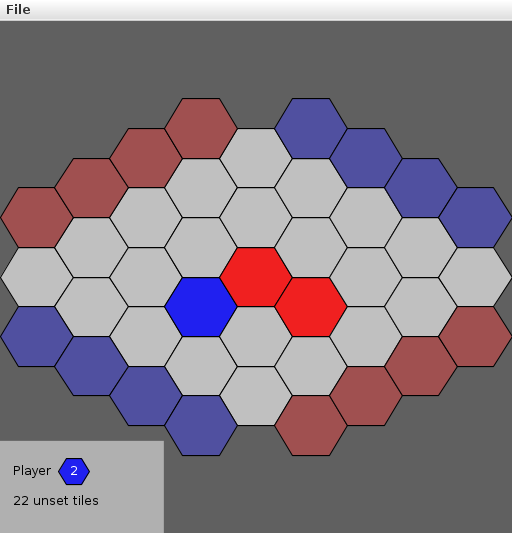
hex, the game
The game of Hex is played on a diamond-shaped board of hexagons. Two players alternate turns by placing their colored stones (red/blue, white/black, etc.) on the board, attempting to make a connection between their respective opposite sides.

dynamic-connectivity solution ⇒ winner
Q: How to determine if a player has won?
A: Model as a dynamic-connectivity problem and use union-find
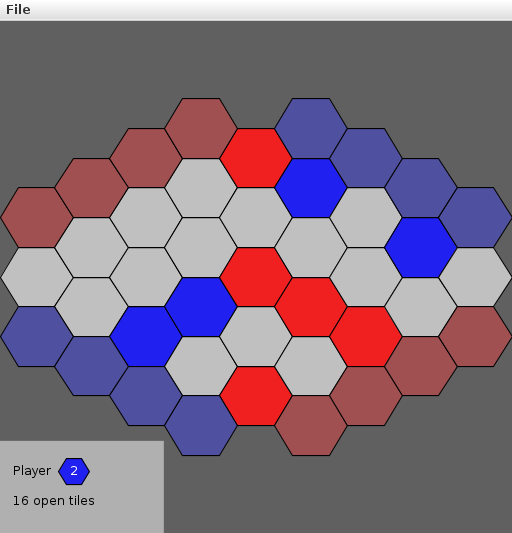
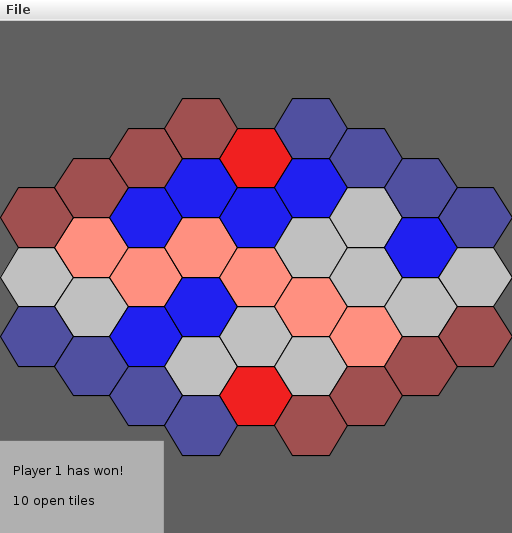
dynamic-connectivity solution ⇒ winner
 |
 |
Create a node for each hexagon tile, named \(0\) to \(N^2-1\)
dynamic-connectivity solution ⇒ winner
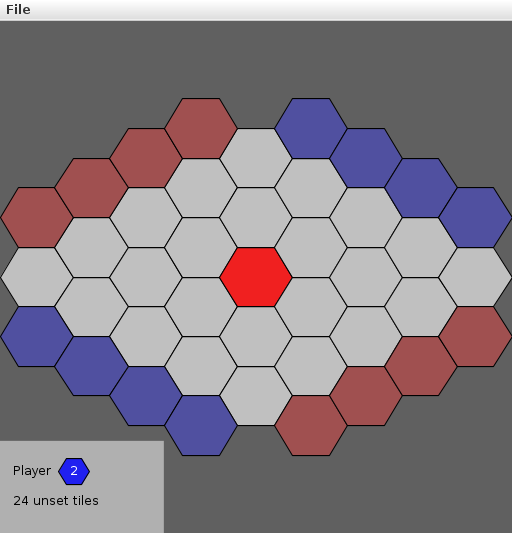 |
 |
Color the node of the player to represent placing a stone
dynamic-connectivity solution ⇒ winner
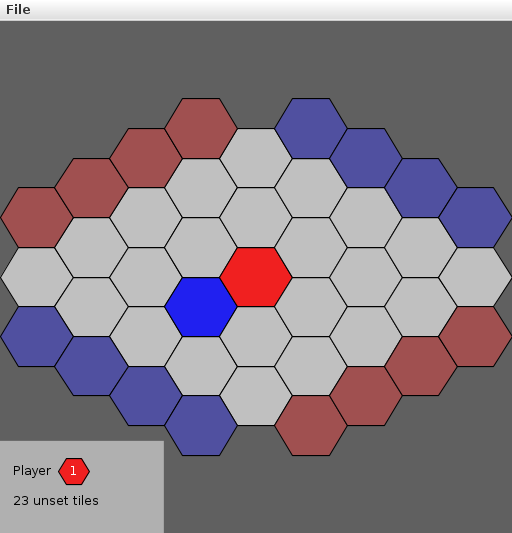 |
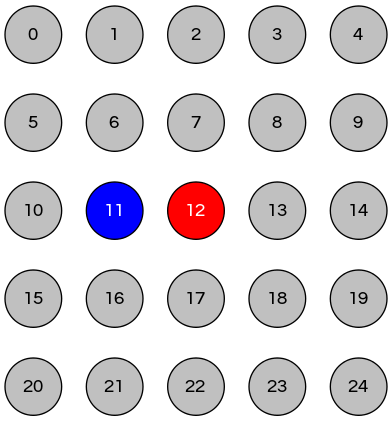 |
Color the node of the player to represent placing a stone
dynamic-connectivity solution ⇒ winner
 |
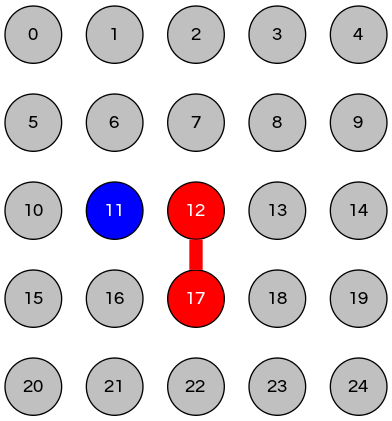 |
Add edge between two adjacent nodes if they are similarly colored
Note: could add up to 6 edges
dynamic-connectivity solution ⇒ winner
 |
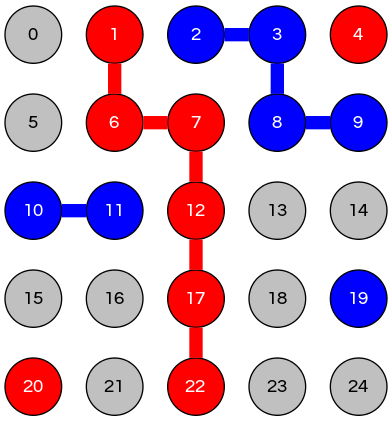 |
A player wins when there is a path between their opposite sides of the board from top–bottom or left–right
Example: check each node at top against each node at bottom
dynamic-connectivity solution ⇒ winner
 |
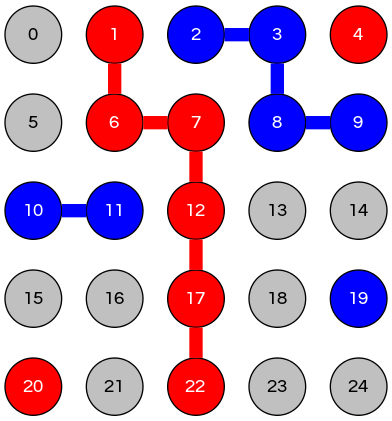 |
How can we check this more efficiently?
dynamic-connectivity solution ⇒ winner
 |
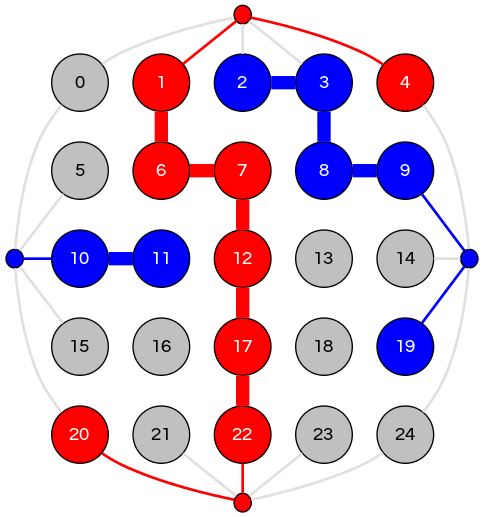 |
Clever trick: introduce 4 virtual nodes, edges where appropriate
A player wins when there is a path between opposite virtual nodes
subtext of today's lecture (and this course)
|
Steps to developing a usable algorithm to solve a computational problem
|
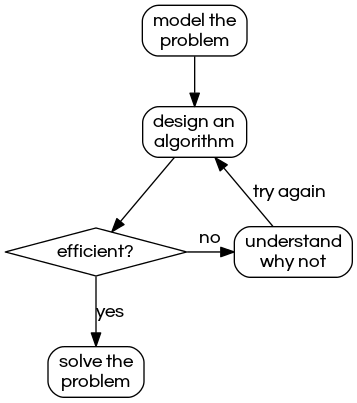 |
This is the scientific method
Mathematical analysis